1. 概述
质谱是化学分析中重要的分析工具。利用质谱可以获得化合物的相对分子质量,并且还可以通过碎片离子峰的位置与强度大小推测更多的分子结构信息。
判定分子离子峰时,由于组成分子的元素存在丰度不一的同位素导致同位素离子峰的出现,一方面增加了分子离子峰的复杂程度,但另一方面,由于同位素质量数和丰度各异,这些同位素离子峰的位置与强度分布也给分子式的确定提供了线索,即可以依据质谱法所测得同位素峰强度分布确定最可能的分子式。由于数十年以前计算能力不发达,复杂分子的同位素峰强度分布计算相对困难,Beynon J. H. et al.于20世纪60年代计算了含C、H、N、O的各种组合的质量数和同位素丰度比,列表成册,用以确定分子式。此表目前仍在广泛使用。
仪器分析课程中,涉及到同位素峰强度比计算的部分,仅要求一些简单分子(如:CHCl3 等)质量数分布的推导,并且进行了大量的忽略,得到的结果为近似值。而事实上,在21世纪的今天,实现beynon表的快速精确计算不费吹灰之力。推导同位素分布的精确表达式,也有助于理解近似表达式。本文将详细阐述复杂分子同位素峰丰度计算原理,对精确和近似表达式进行推导,最终通过python编程实现一个多功能的同位素峰强度分布计算器与beynon表查询器。
2. 同位素峰丰度计算原理
2.1 二项分布与同种元素原子团丰度计算
整个丰度计算原理是基于二项分布的。二项分布是二项式定理的一种特殊形式。其最原始概念是:
如果某事件发生的概率是p,二项分布即N次独立重复试验中该事件发生k次的概率分布。
其数学表达式写成:
P ( x = k ) = C n k ⋅ p k ⋅ ( 1 − p ) n − k P(x=k)=C_n^k\cdot p^k\cdot{(1-p)}^{n-k}
P ( x = k ) = C n k ⋅ p k ⋅ ( 1 − p ) n − k
所有可能发生情况概率之和自然等于1:
∑ k = 0 n P ( x = k ) = ∑ k = 0 n C n k ⋅ p k ⋅ ( 1 − p ) n − k = 1 \sum\limits_{k=0}^n{P(x=k)}=\sum\limits_{k=0}^n{C_n^k\cdot p^k\cdot {(1-p)^{n-k}}=1}
k = 0 ∑ n P ( x = k ) = k = 0 ∑ n C n k ⋅ p k ⋅ ( 1 − p ) n − k = 1
那么如何将该概念迁移到同位素分布中呢?
可以将“该事件”设为某个元素的一个同位素,而将“该事件发生的概率”看作该同位素的丰度,于是上述表述变成:
如果某个元素的一个同位素Isoa 丰度为x1 ,则含N个此种元素的原子团中含有该同位素的个数为k的概率为
P ( x = k ) = C n k ⋅ p k ⋅ ( 1 − p ) n − k P(x=k)=C_n^k\cdot p^k\cdot{(1-p)}^{n-k}
P ( x = k ) = C n k ⋅ p k ⋅ ( 1 − p ) n − k
如果该元素只含有两种同位素Isoa 和Isob ,则上述概率表示Isoa k Isob n-k 占所有可能的组合的比率,即该原子团中Isoa k Isob n-k 的丰度值。
至此,我们迈出了第一步。
上述假设该元素只有两种同位素,那么当同位素有3种、4种、…、n种时,相应的丰度分布计算该如何在二项分布的基础上延伸呢?不妨探讨一下三种同位素的情况。
二项分布的概念可以更加详细地表述如下:
如果某个元素的一个同位素Isoa 丰度为x1 ,则n个此种元素的原子团中含有该同位素的个数为k且Isoa 以外其他同位素任意组合成n-k原子团的概率为
P ( I s o a = k , [ I s o b , I s o c , . . . , I s o i ( i ≠ 0 ) ] = n − k ) = C n k ⋅ x 1 k ⋅ ( 1 − x 1 ) n − k P(Iso^{a}=k,[Iso^{b},Iso^{c},...,Iso^{i(i\not=0)}]=n-k)=C_n^k\cdot{x_1}^k\cdot{(1-x_1)}^{n-k}
P ( I s o a = k , [ I s o b , I s o c , ... , I s o i ( i = 0 ) ] = n − k ) = C n k ⋅ x 1 k ⋅ ( 1 − x 1 ) n − k
当同位素只有两种时,不含有第一种同位素的n-k个原子的任意组合方式只有一种,即n-k个Isob 原子组成的原子团。但是有3种同位素时,不含有第一种同位素的n-k个原子的任意组合方式将不止一种,比如1个Isob 同位素与n-k-1个Isoc 同位素组成的原子团;2个Isob 同位素与n-k-2个Isoc 同位素组成的原子团……以此类推,这种组合方式将共有n-k种,每种组合方式都有其概率并且等于:
P ( I s o b = i , I s o c = n − k − i ) = C n − k i ⋅ x 2 i ⋅ x 3 n − k − i P(Iso^{b}=i,Iso^{c}=n-k-i)=C_{n-k}^{i}\cdot {x_2}^i\cdot {x_3}^{n-k-i}
P ( I s o b = i , I s o c = n − k − i ) = C n − k i ⋅ x 2 i ⋅ x 3 n − k − i
其中,Isoc 的丰度:
x 3 = 1 − x 2 − x 1 x_3=1-x_2-x_1
x 3 = 1 − x 2 − x 1
而所有组合的概率之和,根据二项式定理 (注意:与二项分布不同,因为x 2 + x 3 ≠ 1 x_2+x_3\not=1 x 2 + x 3 = 1
∑ i = 0 n − k P ( x 2 = i , x 3 = n − k − i ) = ∑ i = 0 n − k C n − k k ⋅ x 2 i ⋅ x 3 n − k − i = ( x 2 + x 3 ) n − k = ( 1 − x 1 ) n − k \sum\limits_{i=0}^{n-k}P(x_2=i,x_3=n-k-i)=\sum\limits_{i=0}^{n-k}C_{n-k}^k\cdot{x_2}^i\cdot{x_3}^{n-k-i}={(x_2+x_3)}^{n-k}=(1-x_1)^{n-k}
i = 0 ∑ n − k P ( x 2 = i , x 3 = n − k − i ) = i = 0 ∑ n − k C n − k k ⋅ x 2 i ⋅ x 3 n − k − i = ( x 2 + x 3 ) n − k = ( 1 − x 1 ) n − k
即:
P ( I s o a = k , [ I s o b , I s o c ] = n − k ) = C n k ⋅ x 1 k ⋅ ( 1 − x 1 ) n − k = C n k ⋅ x 1 k ⋅ ∑ i = 0 n − k P ( x 2 = i , x 3 = n − k − i ) = C n k ⋅ x 1 k ⋅ ∑ i = 0 n − k C n − k k ⋅ x 2 i ⋅ x 3 n − k − i \begin{aligned}
P(Iso^{a} &= k,[Iso^{b},Iso^{c}] = n-k) \\&= C_n^k\cdot{x_1}^k\cdot{(1-x_1)}^{n-k}\\ &= C_n^k\cdot{x_1}^k\cdot\sum\limits_{i = 0}^{n-k}P(x_2 = i,x_3 = n-k-i)\\ &= C_n^k\cdot{x_1}^k\cdot\sum\limits_{i = 0}^{n-k}C_{n-k}^k\cdot{x_2}^i\cdot{x_3}^{n-k-i}
\end{aligned}
P ( I s o a = k , [ I s o b , I s o c ] = n − k ) = C n k ⋅ x 1 k ⋅ ( 1 − x 1 ) n − k = C n k ⋅ x 1 k ⋅ i = 0 ∑ n − k P ( x 2 = i , x 3 = n − k − i ) = C n k ⋅ x 1 k ⋅ i = 0 ∑ n − k C n − k k ⋅ x 2 i ⋅ x 3 n − k − i
若想求某个组合的概率,移除求和号可得:
P ( I s o a = k , I s o b = i , I s o c = n − k − i ) = C n k ⋅ x 1 k ⋅ P ( x 2 = i , x 3 = n − k − i ) = C n k ⋅ x 1 k ⋅ C n − k k ⋅ x 2 i ⋅ x 3 n − k − i = C n k ⋅ C n − k k ⋅ x 1 k ⋅ x 2 i ⋅ x 3 n − k − i \begin{aligned}
P(Iso^{a} & = k,Iso^{b} = i,Iso^{c} = n-k-i)\\&= C_n^k\cdot{x_1}^k\cdot P(x_2 = i,x_3 = n-k-i)\\
& = C_n^k\cdot{x_1}^k\cdot C_{n-k}^k\cdot{x_2}^i\cdot{x_3}^{n-k-i}\\
& = C_n^k\cdot C_{n-k}^k\cdot{x_1}^k\cdot{x_2}^i\cdot{x_3}^{n-k-i}
\end{aligned}
P ( I s o a = k , I s o b = i , I s o c = n − k − i ) = C n k ⋅ x 1 k ⋅ P ( x 2 = i , x 3 = n − k − i ) = C n k ⋅ x 1 k ⋅ C n − k k ⋅ x 2 i ⋅ x 3 n − k − i = C n k ⋅ C n − k k ⋅ x 1 k ⋅ x 2 i ⋅ x 3 n − k − i
该概率即为Isoa ,Isob ,Isoc 分别有k,i,n-k-i个时的概率。
至此,我们成功将二项分布推广到了“三项分布”。那么,根据上述原理,推导“n项分布”也就相当容易了。只需将上个公式最后一个同位素看作除其之前的所有同位素之外的同位素任意组合形成的原子团即可。
由此推出4种同位素时:
P ( I s o a = k , I s o b = i , I s o c = j , I s o d = n − k − i − j ) = C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ x 4 n − k − i − j P(Iso^{a}=k,Iso^{b}=i,Iso^{c}=j,Iso^{d}=n-k-i-j)=C_n^k\cdot C_{n-k}^i\cdot C_{n-k-i}^j\cdot{x_1}^k\cdot{x_2}^i\cdot{x_3}^j\cdot{x_4}^{n-k-i-j}
P ( I s o a = k , I s o b = i , I s o c = j , I s o d = n − k − i − j ) = C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ x 4 n − k − i − j
n种同位素时:
P ( I s o a = k , I s o b = i , . . . , I s o X , I s o Y = n − ∑ ϵ = 所有 Y 之前 I s o ϵ ) = P ( M = A ( I s o a ) ⋅ k + A ( I s o b ) ⋅ i + . . . + A ( I s o Y ) ⋅ ( n − ∑ ϵ = 所有 Y 之前 ) ) = C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ . . . ⋅ C n − ∑ ϵ = 所有 X 之前 I s o ϵ j ⋅ x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ . . . ⋅ x n − 1 I s o X ⋅ x n I s o Y \begin{aligned}
P&\left( Iso^{a} = k,Iso^{b} = i,...,Iso^{X},Iso^{Y} = n-\sum\limits_{\epsilon = \text{所有}Y\text{之前}}Iso^{\epsilon}\right)
\\ &= P\left( M = A(Iso^{a})\cdot k+A(Iso^{b})\cdot i+...+A(Iso^{Y})\cdot\left( n-\sum\limits_{\epsilon = \text{所有}Y\text{之前}}\right)\right)
\\ &= C_n^k\cdot C_{n-k}^i\cdot C_{n-k-i}^j\cdot ... \cdot C_{n-\sum_{\epsilon = \text{所有}X\text{之前}}Iso^{\epsilon}}^{j}\cdot {x_1}^k\cdot{x_2}^i\cdot{x_3}^j\cdot ... \cdot{x_{n-1}}^{Iso^{X}}\cdot{x_n}^{Iso^{Y}}
\end{aligned}
P ( I s o a = k , I s o b = i , ... , I s o X , I s o Y = n − ϵ = 所有 Y 之前 ∑ I s o ϵ ) = P ( M = A ( I s o a ) ⋅ k + A ( I s o b ) ⋅ i + ... + A ( I s o Y ) ⋅ ( n − ϵ = 所有 Y 之前 ∑ ) ) = C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ ... ⋅ C n − ∑ ϵ = 所有 X 之前 I s o ϵ j ⋅ x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ ... ⋅ x n − 1 I s o X ⋅ x n I s o Y
其中A(Isoa )代表Isoa 的质量数。至此,我们推出了同种元素不同同位素组成的原子团丰度计算公式,最核心的工作已经完成。那么如何将不同种元素结合起来,计算整个分子的同位素分布呢?
2.2 不同种元素同位素分子丰度计算
事实上,我们可以将上述同种元素的原子团看作一个整体,或者说,一个含有不同丰度“同位素”的“新元素”,这样,这个“新元素”就可以和其他的“新元素”组合,问题转变为简单组合问题。
比如,计算苯的同位素分子丰度时,将6个碳看作一个原子团,将6个氢看作另一个原子团,分别计算它们的“同位素”丰度:
“C6”原子团(丰度极低的“同位素”未列出,下同):
质量数
差值
丰度
72
0
93.53913
73
1
6.28242
74
2
0.17581
75
3
0.00262
76
4
0.00002
“H6”原子团:
质量数
差值
丰度
6
0
99.91003
7
1
0.08993
8
2
0.00003
…
…
…
将每一个“C6”原子团的“同位素”与“H6”的组合:
质量数
丰度
72+6
93.53913×99.91003=93.45497
72+7
93.53913×0.08993=0.08412
72+8
…
73+6
…
…
…
将所有质量数相同的新原子团丰度相加,最终即得苯的同位素分布:
质量数
差值
丰度
78
0
93.45497
79
1
6.36089
80
2
0.18134
…
…
…
即对于仅含两种元素的分子M1 ,M2 ,设它们质量数最小的同位素原子团的质量数为M1,b ,M2,b ,则这两个原子团相互结合成新原子团M2’ 且其质量数为M 1 , b + M 2 , b + α M_{1,b}+M_{2,b}+\alpha M 1 , b + M 2 , b + α
P ( M 2 ′ = M 1 , b + M 2 , b + α ) = ∑ z = 0 α P ( M 1 , b + z ) ⋅ P ( M 2 , b + α − z ) P(M_{2\rq{}}=M_{1,b}+M_{2,b}+\alpha )=\sum\limits_{z=0}^{\alpha}P(M_{1,b}+z)\cdot P(M_{2,b}+\alpha -z)
P ( M 2 ′ = M 1 , b + M 2 , b + α ) = z = 0 ∑ α P ( M 1 , b + z ) ⋅ P ( M 2 , b + α − z )
当i=0时,M2’ =M2,b .
如果分子中含有三个及以上元素,则可以将前两个原子团组合生成的新的原子团与另一个元素组成的原子团组合成M3’ :
P ( M 3 ′ = M 2 , b + M 3 , b + β ) = ∑ y = 0 β P ( M 2 , b + y ) ⋅ P ( M 3 , b + β − y ) = ∑ y = 0 β P ( M 3 , b + β − y ) ⋅ P ( M 1 , b + M 2 , b + y ) = ∑ y = 0 β ∑ z = 0 y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 + β − y ) \begin{aligned}
P(M_{3'} &= M_{2,b}+M_{3,b}+\beta)
\\& = \sum\limits_{y = 0}^{\beta}P(M_{2,b}+y)\cdot P(M_{3,b}+\beta -y)
\\& = \sum\limits_{y = 0}^{\beta}P(M_{3,b}+\beta -y)\cdot P(M_{1,b}+M_{2,b}+y)
\\& = \sum\limits_{y = 0}^{\beta}\sum\limits_{z = 0}^{y}P(M_{1,b}+z)\cdot P(M_{2,b}+y-z)\cdot P(M_3+\beta -y)
\end{aligned}
P ( M 3 ′ = M 2 , b + M 3 , b + β ) = y = 0 ∑ β P ( M 2 , b + y ) ⋅ P ( M 3 , b + β − y ) = y = 0 ∑ β P ( M 3 , b + β − y ) ⋅ P ( M 1 , b + M 2 , b + y ) = y = 0 ∑ β z = 0 ∑ y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 + β − y )
依此类推,不断组合直至形成最后一个原子团Mn’ 即分子本身,该分子的同位素分布也就自然得到了。
P ( M n ′ = M n − 1 ′ , b + M n , b + θ ) = ∑ π = 0 θ P ( M n − 1 ′ , b + θ ) ⋅ P ( M n , b + θ − π ) = ∑ π = 0 θ . . . ∑ y = 0 β ∑ z = 0 y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 , b + β − y ) ⋅ . . . ⋅ P ( M n , b + θ − π ) \begin{aligned}
P(M_{n'}&=M_{n-1',b}+M_{n,b}+\theta )
\\&=\sum\limits_{\pi=0}^{\theta}P(M_{n-1',b}+\theta)\cdot P(M_{n,b}+\theta -\pi)
\\&=\sum\limits_{\pi=0}^{\theta}...\sum\limits_{y=0}^{\beta}\sum\limits_{z=0}^{y}P(M_{1,b}+z)\cdot P(M_{2,b}+y-z)\cdot P(M_{3,b}+\beta - y)\cdot ...\cdot P(M_{n,b}+\theta - \pi)
\end{aligned}
P ( M n ′ = M n − 1 ′ , b + M n , b + θ ) = π = 0 ∑ θ P ( M n − 1 ′ , b + θ ) ⋅ P ( M n , b + θ − π ) = π = 0 ∑ θ ... y = 0 ∑ β z = 0 ∑ y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 , b + β − y ) ⋅ ... ⋅ P ( M n , b + θ − π )
2.3 近似公式的导出
在实践中,常用到计算M+1/M,M+2/M峰强度比的近似公式:
对于分子式C w H x N y O z S s C_wH_xN_yOzS_s C w H x N y O z S s
M+1/M峰相对强度计算公式如下:
M + 1 M % = [ w ⋅ α 2 α 1 + x ⋅ β 2 β 1 + y ⋅ γ 2 γ 1 + z ⋅ δ 2 δ 1 + s ⋅ ε 2 ε 1 ] × 100 % \frac{M+1}{M} \%=\left[w \cdot \frac{\alpha_{2}}{\alpha_{1}}+x \cdot \frac{\beta_{2}}{\beta_{1}}+y \cdot \frac{\gamma_{2}}{\gamma_{1}}+z \cdot \frac{\delta_{2}}{\delta_{1}}+s \cdot \frac{\varepsilon_{2}}{\varepsilon_{1}}\right] \times 100 \%
M M + 1 % = [ w ⋅ α 1 α 2 + x ⋅ β 1 β 2 + y ⋅ γ 1 γ 2 + z ⋅ δ 1 δ 2 + s ⋅ ε 1 ε 2 ] × 100%
M+2/M峰相对强度计算公式如下:
M + 2 M % = { 1 2 [ w ( w − 1 ) ( α 2 α 1 ) 2 + x ( x − 1 ) ( β 2 β 1 ) 2 + y ( y − 1 ) ( γ 2 γ 1 ) 2 + z ( z − 1 ) ( δ 2 δ 1 ) 2 + s ( s − 1 ) ( ε 2 ε 1 ) 2 ] + s ⋅ ε 3 ε 1 } × 100 % \frac{M+2}{M} \%=\left\{\frac{1}{2}\left[w(w-1)\left(\frac{\alpha_{2}}{\alpha_{1}}\right)^{2}+x(x-1)\left(\frac{\beta_{2}}{\beta_{1}}\right)^{2}+y(y-1)\left(\frac{\gamma_{2}}{\gamma_{1}}\right)^{2}+z(z-1)\left(\frac{\delta_{2}}{\delta_{1}}\right)^{2}+s(s-1)\left(\frac{\varepsilon_{2}}{\varepsilon_{1}}\right)^{2}\right]+s \cdot \frac{\varepsilon_{3}}{\varepsilon_{1}}\right\}\times 100\%
M M + 2 % = { 2 1 [ w ( w − 1 ) ( α 1 α 2 ) 2 + x ( x − 1 ) ( β 1 β 2 ) 2 + y ( y − 1 ) ( γ 1 γ 2 ) 2 + z ( z − 1 ) ( δ 1 δ 2 ) 2 + s ( s − 1 ) ( ε 1 ε 2 ) 2 ] + s ⋅ ε 1 ε 3 } × 100%
其中,α 2 , α 1 , β 2 , β 1 , γ 2 , γ 1 , σ 2 , σ 1 \alpha_2,\alpha_1,\beta_2,\beta_1,\gamma_2,\gamma_1,\sigma_2,\sigma_1 α 2 , α 1 , β 2 , β 1 , γ 2 , γ 1 , σ 2 , σ 1 ε 3 , ε 2 , ε 1 \varepsilon_3,\varepsilon_2,\varepsilon_1 ε 3 , ε 2 , ε 1
这两个公式如何通过近似得到?相信通过上文的推导,读者已经可以自己推出。
首先,我们仍要将一个分子按照不同元素拆分为原子团看待。
M+1同位素分子的含量显然为所有原子团中任意一个原子团的质量数为M’+1且其他原子团质量数均为M’的分子含量之和。
对于每一个原子团而言,可以计算出该原子团质量数为M+1“同位素”与质量数为M“同位素”含量之比:
对于w个C构成的原子团,w+1“同位素”丰度即含有w-1个12C与1个13C的丰度:
ω M + 1 = C w 1 α 1 w − 1 ⋅ C 1 0 α 2 1 = C w 1 α 1 w − 1 α 2 = w α 1 w − 1 α 2 \omega_{M+1}=C_{w}^{1} \alpha_{1}^ {w-1} \cdot C_{1}^{0} \alpha_{2}^{1}=C_{w}^{1} \alpha_{1}^{ w-1} \alpha_{2}=w \alpha_{1}^{ w-1 }\alpha_{2}
ω M + 1 = C w 1 α 1 w − 1 ⋅ C 1 0 α 2 1 = C w 1 α 1 w − 1 α 2 = w α 1 w − 1 α 2
相比于ω M = C w o α 1 w = α 1 w \omega_{M}=C_{w}^{o} \alpha_{1}^{w}=\alpha_{1}^{w} ω M = C w o α 1 w = α 1 w
ω M + 1 ω M = w α 1 w − 1 α 2 α 1 w = w ⋅ α 2 α 1 \frac{\omega_{M+1}}{\omega_{M}}=\frac{w \alpha_{1}^{ w-1} \alpha_{2}}{\alpha_{1}^ w}=w \cdot \frac{\alpha_{2}}{\alpha_{1}}
ω M ω M + 1 = α 1 w w α 1 w − 1 α 2 = w ⋅ α 1 α 2
同理可以得到对于H,N,O,S,它们所构成的原子团M+1/M之比为为x ⋅ β 2 β 1 , y ⋅ γ 2 γ 1 , z ⋅ δ 2 δ 1 , s ⋅ ε 2 ε 1 x \cdot \frac{\beta_{2}}{\beta_{1}}, y \cdot \frac{\gamma_{2}}{\gamma_{1}}, z \cdot \frac{\delta_{2}}{\delta_{1}}, s \cdot \frac{\varepsilon_{2}}{\varepsilon_{1}} x ⋅ β 1 β 2 , y ⋅ γ 1 γ 2 , z ⋅ δ 1 δ 2 , s ⋅ ε 1 ε 2
M + 1 M % = [ w ⋅ α 2 α 1 + x ⋅ β 2 β 1 + y ⋅ γ 2 γ 1 + z ⋅ δ 2 δ 1 + s ⋅ ε 2 ε 1 ] × 100 % \frac{M+1}{M} \%=\left[w \cdot \frac{\alpha_{2}}{\alpha_{1}}+x \cdot \frac{\beta_{2}}{\beta_{1}}+y \cdot \frac{\gamma_{2}}{\gamma_{1}}+z \cdot \frac{\delta_{2}}{\delta_{1}}+s \cdot \frac{\varepsilon_{2}}{\varepsilon_{1}}\right] \times 100 \%
M M + 1 % = [ w ⋅ α 1 α 2 + x ⋅ β 1 β 2 + y ⋅ γ 1 γ 2 + z ⋅ δ 1 δ 2 + s ⋅ ε 1 ε 2 ] × 100%
在计算M+2/M时,为方便计算,还需要进行进一步的忽略,即忽略分子中含有两种不同元素原子团的M+1“同位素”。忽略后,按照上述原理:
对于w个C构成的原子团,A+2“同位素”丰度即含有w-2个12C与2个13C的丰度:
ω M + 2 = C w 2 α 1 w − 2 ⋅ C 2 0 α 2 2 = C w 2 α 1 w − 2 α 2 2 = 1 2 ⋅ w ( w − 1 ) α 1 w − 2 α 2 2 \omega_{M+2}=C_{w}^{2} \alpha_{1}^{ w-2} \cdot C_{2}^{0} \alpha_{2}^{2}=C_{w}^{2} \alpha_{1}^{w-2} \alpha_{2}^{2}=\frac{1}{2} \cdot w(w-1) \alpha_{1}^{w-2} \alpha_{2}^{2}
ω M + 2 = C w 2 α 1 w − 2 ⋅ C 2 0 α 2 2 = C w 2 α 1 w − 2 α 2 2 = 2 1 ⋅ w ( w − 1 ) α 1 w − 2 α 2 2
相比于ω M = C w o α 1 w = α 1 w \omega_{M}=C_{w}^{o} \alpha_{1}^{w}=\alpha_{1}^{w} ω M = C w o α 1 w = α 1 w
ω M + 2 ω M = 1 2 ⋅ w ( w − 1 ) α 1 w − 2 α 2 2 α 1 w = 1 2 ⋅ w ( w − 1 ) ⋅ ( α 2 α 1 ) 2 \frac{\omega_{M+2}}{\omega_{M}}=\frac{\frac{1}{2} \cdot w(w-1) \alpha_{1}^{w-2} \alpha_{2}^{2}}{\alpha_{1} w}=\frac{1}{2} \cdot w(w-1) \cdot\left(\frac{\alpha_{2}}{\alpha_{1}}\right)^{2}
ω M ω M + 2 = α 1 w 2 1 ⋅ w ( w − 1 ) α 1 w − 2 α 2 2 = 2 1 ⋅ w ( w − 1 ) ⋅ ( α 1 α 2 ) 2
对于某些A+2同位素丰度较大不能忽略不计的元素如S,其构成的原子团M+2/M的计算分为两部分:
对于s个硫构成的原子团,A+2“同位素”丰度即含有s-2个32S和2个33S的概率和含有s-1个32S和1个34S的概率之和:
ω M + 2 = C s 2 ε 1 s − 2 ⋅ C 2 0 ε 2 2 + C s 1 ε 1 s − 1 ⋅ C 1 0 ε 3 1 = C s 2 ε 1 s − 2 ε 2 2 + C s 1 ε 1 s − 1 ε 3 = 1 2 ⋅ s ( s − 1 ) ε 1 s − 2 ε 2 2 + s ε 1 s − 1 ε 3 \omega_{M+2}=C_{s}^{2} \varepsilon_{1}^{s-2} \cdot C_{2}^{0} \varepsilon_{2}^{2}+C_{s}^{1} \varepsilon_{1}^{s-1} \cdot C_{1}^{0} \varepsilon_{3}^{1}=C_{s}^{2} \varepsilon_{1}^{s-2} \varepsilon_{2}^{2}+C_{s}^{1} \varepsilon_{1}^{s-1} \varepsilon_{3}=\frac{1}{2} \cdot s(s-1) \varepsilon_{1}^{s-2} \varepsilon_{2}^{2}+s \varepsilon_{1}^{s-1} \varepsilon_{3}
ω M + 2 = C s 2 ε 1 s − 2 ⋅ C 2 0 ε 2 2 + C s 1 ε 1 s − 1 ⋅ C 1 0 ε 3 1 = C s 2 ε 1 s − 2 ε 2 2 + C s 1 ε 1 s − 1 ε 3 = 2 1 ⋅ s ( s − 1 ) ε 1 s − 2 ε 2 2 + s ε 1 s − 1 ε 3
相比于ω M = C w o ε 1 s = ε 1 s \omega_{M}=C_{w}^{o} \varepsilon_{1}^{s}=\varepsilon_{1}^{s} ω M = C w o ε 1 s = ε 1 s
ω M + 2 ω M = 1 2 ⋅ s ( s − 1 ) ε 1 s − 2 ε 2 2 + s ε 1 s − 1 ε 2 ε 1 s = 1 2 ⋅ s ( s − 1 ) ( ε 2 ε 1 ) 2 + s ⋅ ε 3 ε 1 \frac{\omega_{M+2}}{\omega_{M}}=\frac{\frac{1}{2} \cdot s(s-1) \varepsilon_{1}^{s-2} \varepsilon_{2}^{2}+s \varepsilon_{1}^{s-1} \varepsilon_{2}}{\varepsilon_{1}^{s}}=\frac{1}{2} \cdot s(s-1)\left(\frac{\varepsilon_{2}}{\varepsilon_{1}}\right)^{2}+s \cdot \frac{\varepsilon_{3}}{\varepsilon_{1}}
ω M ω M + 2 = ε 1 s 2 1 ⋅ s ( s − 1 ) ε 1 s − 2 ε 2 2 + s ε 1 s − 1 ε 2 = 2 1 ⋅ s ( s − 1 ) ( ε 1 ε 2 ) 2 + s ⋅ ε 1 ε 3
进行相关近似后,即得M+2/M算式:
M + 2 M % = { 1 2 [ w ( w − 1 ) ( α 2 α 1 ) 2 + x ( x − 1 ) ( β 2 β 1 ) 2 + y ( y − 1 ) ( γ 2 γ 1 ) 2 + z ( z − 1 ) ( δ 2 δ 1 ) 2 + s ( s − 1 ) ( ε 2 ε 1 ) 2 ] + s ⋅ ε 3 ε 1 } × 100 % \frac{M+2}{M} \%=\left\{\frac{1}{2}\left[w(w-1)\left(\frac{\alpha_{2}}{\alpha_{1}}\right)^{2}+x(x-1)\left(\frac{\beta_{2}}{\beta_{1}}\right)^{2}+y(y-1)\left(\frac{\gamma_{2}}{\gamma_{1}}\right)^{2}+z(z-1)\left(\frac{\delta_{2}}{\delta_{1}}\right)^{2}+s(s-1)\left(\frac{\varepsilon_{2}}{\varepsilon_{1}}\right)^{2}\right]+s \cdot \frac{\varepsilon_{3}}{\varepsilon_{1}}\right\}\times 100\%
M M + 2 % = { 2 1 [ w ( w − 1 ) ( α 1 α 2 ) 2 + x ( x − 1 ) ( β 1 β 2 ) 2 + y ( y − 1 ) ( γ 1 γ 2 ) 2 + z ( z − 1 ) ( δ 1 δ 2 ) 2 + s ( s − 1 ) ( ε 1 ε 2 ) 2 ] + s ⋅ ε 1 ε 3 } × 100%
至此我们得到了计算M+1/M,M+2/M同位素峰强度比的近似算式。
基于上述计算方法即可设计程序。请见第三节。
3 python编程实现
3.1 给定分子式计算同位素分子分布
我们希望通过函数calc,输入分子构成,输出其同位素分子分布。比如,输入分子式“CHCl3”,使用分子式解码器decode_formula转换为原子序数与原子个数的组合[6,1,1,1,17,3]后,作为calc函数的参数输入。calc函数返回一个字典,键值对分别为同位素分子的质量数与其丰度值:
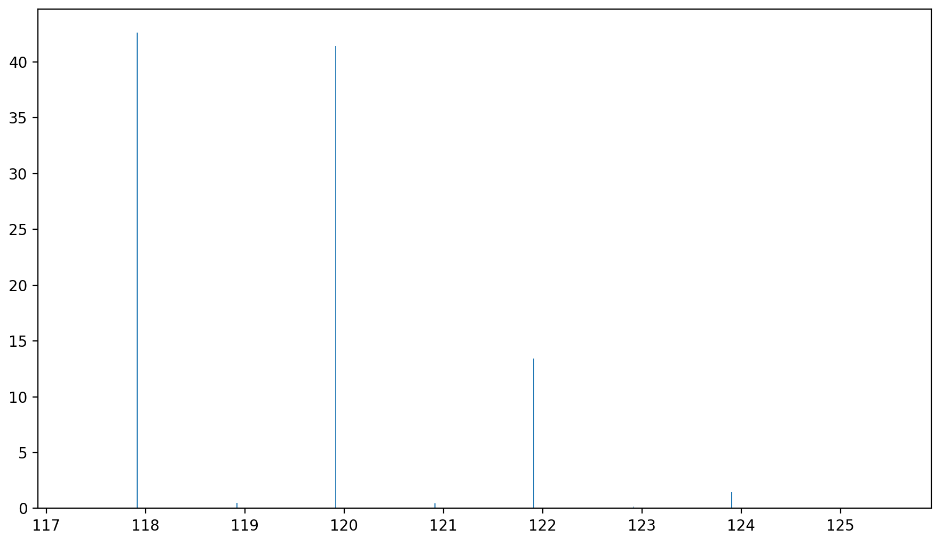
1 2 3 4 5 6 7 8 9 10 11 { 118 : 0.4260483196792795 , 120 : 0.4140905757690965 , 122 : 0.13415638030779484 , 124 : 0.014488020913903278 ,119 : 0.004833066217991269 , 121 : 0.00469741018221553 , 123 : 0.0015218539276951413 , 125 : 0.00016434867209806303 , 126 : 2.4329925998491497e-08 }
那么如何实现该函数呢?据前文所述,计算整个分子的同位素峰强度分布分两步,第一步是计算所有元素构成的原子团的分布,然后再将这些原子团组合。所以首先应建立一个循环,将所有原子团的分布计算出来。
1 for keys in range (0 , len (args), 2 ):
在循环内部,每计算一个原子团,需要按顺序读取该列表中的两个元素:
1 2 atomic_num = args[keys] proton_num = args[keys + 1 ]
我们需要获取字典中的所有键,也就是所有可能的原子团“同位素”的质量数才能建立字典:
1 2 3 masses = set () this_isotope = isotope_info[atomic_num]['isotopes' ] isotope_num = len (this_isotope)
然后,我们需要根据同位素的个数以及该原子团的原子个数获得所有可能的排列组合:
1 combinations = get_combination(isotope_num, proton_num)
举例说明:如果该元素有2种同位素且原子团中含有2个原子,则get_combination函数会返回[[0, 2], [1, 1], [2, 0]],即意味着所有可能的组合为:0个A同位素与2个B同位素、1个A同位素与1个B同位素,2个A同位素与0个B同位素。同理,3种同位素4个原子的情况共有:[[0, 0, 4], [0, 1, 3], [0, 2, 2], [0, 3, 1], [0, 4, 0], [1, 0, 3], [1, 1, 2], [1, 2, 1], [1, 3, 0], [2, 0, 2], [2, 1, 1], [2, 2, 0], [3, 0, 1], [3, 1, 0], [4, 0, 0]],读者可以自行验证。计算并输出所有组合的函数get_combination的编写需要运用栈有关的知识,这里不再赘述。
获取所有组合方式后,便可以计算并保存所有可能出现的质量数了:
1 2 3 for each_combination in combinations: mass_number = get_mass_number(each_combination, this_isotope) masses.add(mass_number)
然后,我们根据质量数建立字典,字典的所有值均设定为0:
1 2 3 mass_dict = dict () for i in masses: mass_dict.update({i: 0.0 })
接下来,就要根据公式
P ( M n ′ = M n − 1 ′ , b + M n , b + θ ) = ∑ π = 0 θ P ( M n − 1 ′ , b + θ ) ⋅ P ( M n , b + θ − π ) = ∑ π = 0 θ . . . ∑ y = 0 β ∑ z = 0 y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 , b + β − y ) ⋅ . . . ⋅ P ( M n , b + θ − π ) \begin{aligned}
P(M_{n'}&=M_{n-1',b}+M_{n,b}+\theta )
\\&=\sum\limits_{\pi=0}^{\theta}P(M_{n-1',b}+\theta)\cdot P(M_{n,b}+\theta -\pi)
\\&=\sum\limits_{\pi=0}^{\theta}...\sum\limits_{y=0}^{\beta}\sum\limits_{z=0}^{y}P(M_{1,b}+z)\cdot P(M_{2,b}+y-z)\cdot P(M_{3,b}+\beta - y)\cdot ...\cdot P(M_{n,b}+\theta - \pi)
\end{aligned}
P ( M n ′ = M n − 1 ′ , b + M n , b + θ ) = π = 0 ∑ θ P ( M n − 1 ′ , b + θ ) ⋅ P ( M n , b + θ − π ) = π = 0 ∑ θ ... y = 0 ∑ β z = 0 ∑ y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 , b + β − y ) ⋅ ... ⋅ P ( M n , b + θ − π )
来计算对应的概率了。
我们已经获取了所有可能的组合,接下来就要遍历这些组合:
1 for each_combination in combinations:
首先,新建变量probability用于保存计算所得的概率值,并初始化为:
1 probability = 0.01 ** proton_num
这是因为数据库中所有的丰度值均是以百分比的形式表示,比如H的同位素信息:
1 2 3 4 'isotopes' : [ {'mass_num' : 1 , 'accurate_mass_num' : 1.007825 , 'abundance' : 99.985 }, {'mass_num' : 2 , 'accurate_mass_num' : 2.014102 , 'abundance' : 0.015 } ]
然后,需要要计算公式中n,n-k,n-k-i,…的值,这其实就是将组合中的元素倒序逐个累加:
1 2 3 cumulative_combination = each_combination.copy() for i in range (len (each_combination) - 1 , 0 , -1 ): cumulative_combination[i - 1 ] += cumulative_combination[i]
然后计算
C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ . . . ⋅ C n − ∑ ϵ = 所有 X 之前 I s o ϵ j ⋅ x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ . . . ⋅ x n − 1 I s o X ⋅ x n I s o Y C_n^k\cdot C_{n-k}^i\cdot C_{n-k-i}^j\cdot ... \cdot C_{n-\sum_{\epsilon = \text{所有}X\text{之前}}Iso^{\epsilon}}^{j}\cdot {x_1}^k\cdot{x_2}^i\cdot{x_3}^j\cdot ... \cdot{x_{n-1}}^{Iso^{X}}\cdot{x_n}^{Iso^{Y}}
C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ ... ⋅ C n − ∑ ϵ = 所有 X 之前 I s o ϵ j ⋅ x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ ... ⋅ x n − 1 I s o X ⋅ x n I s o Y
中的组合部分:
C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ . . . ⋅ C n − ∑ ϵ = 所有 X 之前 I s o ϵ j C_n^k\cdot C_{n-k}^i\cdot C_{n-k-i}^j\cdot ... \cdot C_{n-\sum_{\epsilon = \text{所有}X\text{之前}}Iso^{\epsilon}}^{j}
C n k ⋅ C n − k i ⋅ C n − k − i j ⋅ ... ⋅ C n − ∑ ϵ = 所有 X 之前 I s o ϵ j
再计算概率部分:
x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ . . . ⋅ x n − 1 I s o X ⋅ x n I s o Y {x_1}^k\cdot{x_2}^i\cdot{x_3}^j\cdot ... \cdot{x_{n-1}}^{Iso^{X}}\cdot{x_n}^{Iso^{Y}}
x 1 k ⋅ x 2 i ⋅ x 3 j ⋅ ... ⋅ x n − 1 I s o X ⋅ x n I s o Y
1 2 for i in range (len (each_combination)): probability *= this_isotope[i]['abundance' ] ** each_combination[i]
最后将所得概率加到该组合对应的质量数中:
1 2 probability += mass_dict[get_mass_number(each_combination, this_isotope)] mass_dict.update({get_mass_number(each_combination, this_isotope): probability})
至所有组合遍历结束,一个原子团的同位素分布也就计算完毕了。将计算结果存入列表中:
1 element_list.append(mass_dict)
第一步的计算到此结束,接下来是按照
P ( M n ′ = M n − 1 ′ , b + M n , b + θ ) = ∑ π = 0 θ P ( M n − 1 ′ , b + θ ) ⋅ P ( M n , b + θ − π ) = ∑ π = 0 θ . . . ∑ y = 0 β ∑ z = 0 y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 , b + β − y ) ⋅ . . . ⋅ P ( M n , b + θ − π ) \begin{aligned}
P(M_{n'}&=M_{n-1',b}+M_{n,b}+\theta )
\\&=\sum\limits_{\pi=0}^{\theta}P(M_{n-1',b}+\theta)\cdot P(M_{n,b}+\theta -\pi)
\\&=\sum\limits_{\pi=0}^{\theta}...\sum\limits_{y=0}^{\beta}\sum\limits_{z=0}^{y}P(M_{1,b}+z)\cdot P(M_{2,b}+y-z)\cdot P(M_{3,b}+\beta - y)\cdot ...\cdot P(M_{n,b}+\theta - \pi)
\end{aligned}
P ( M n ′ = M n − 1 ′ , b + M n , b + θ ) = π = 0 ∑ θ P ( M n − 1 ′ , b + θ ) ⋅ P ( M n , b + θ − π ) = π = 0 ∑ θ ... y = 0 ∑ β z = 0 ∑ y P ( M 1 , b + z ) ⋅ P ( M 2 , b + y − z ) ⋅ P ( M 3 , b + β − y ) ⋅ ... ⋅ P ( M n , b + θ − π )
将所有原子团组合起来。由于公式中含有多个求和号,故采用上述循环的办法,两个原子团组成一个新的原子团,该原子团再结合原子团,以此类推。
1 2 3 4 5 6 7 8 9 10 11 12 13 for i in range (len (element_list) - 1 ): new_mass_dict = dict () for mass1, abundance1 in element_list[i].items(): for mass2, abundance2 in element_list[i + 1 ].items(): new_mass_dict.update({mass1 + mass2: 0.0 }) for mass1, abundance1 in element_list[i].items(): for mass2, abundance2 in element_list[i + 1 ].items(): probability = abundance1 * abundance2 probability += new_mass_dict[mass1 + mass2] new_mass_dict.update({mass1 + mass2: probability}) element_list[i + 1 ] = new_mass_dict.copy()
最后,返回最后一个Mn’ 值,也就是同位素分子的分布:
1 2 element_list = element_list[-1 ] return element_list
至此,calc函数编写完毕。
1 2 3 <<CHCl3 Formula M M+1 M+2 M+3 CHCl3 42.60 % 0.48 % 41.41 % 0.47 %
还可以添加参数以M+x/M相对强度的形式显示:
1 2 3 <<CHCl3 -r Formula M+1/M M+2/M M+3/M CHCl3 1.13 % 97.19 % 1.10 %
也可以输出更多、或计算更精确的质量分布:
1 2 3 4 5 6 7 8 9 10 <<CHCl3 -l CHCl3 M = 119.37674118 |M+0| 42.6048319679 % 119 |M+1| 0.4833066218 % 120 |M+2| 41.4090575769 % 121 |M+3| 0.4697410182 % 122 |M+4| 13.4156380308 % 123 |M+5| 0.1521853928 % 124 |M+6| 1.4488020914 % 125 |M+7| 0.0164348672 %
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 <<CHCl3 -a CHCl3 M = 119.37674117.9143840 42.6048319679 % 118.9177390 0.4769149383 % 118.9206610 0.0063916835 % 119.9114340 41.4089860289 % 119.9240160 0.0000715480 % 120.9147890 0.4635287385 % 120.9177110 0.0062122797 % 121.9084840 13.4155684910 % 121.9210660 0.0000695397 % 122.9118390 0.1501727556 % 122.9147610 0.0020126372 % 123.9055340 1.4487795621 % 123.9181160 0.0000225293 % 124.9088890 0.0162175177 % 124.9118110 0.0002173495 %
甚至可以根据强度分布作一张模拟质谱图:
3.2 贝农表查询的实现
得到一张质谱图后,我们往往很难由分子离子峰直接确定分子式,而是通过查询beynon表找到符合该质量数的分子后,比对其同位素峰的相对强度比以确定最可能的分子式。所以形成了一个新的需求:*输入一个质量数,输出所有符合该质量数的分子式并计算同位素峰的强度分布。*比如,质谱质量数为102处测定发现有分子离子峰,则输入102,期望程序输出以下结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 <<102 -r M = 102 Formula M+1/M M+2/M M+3/M C2H6N4O 3.84 % 0.26 % 0.01 % C3H4NO3 3.90 % 0.67 % 0.02 % C3H6N2O2 4.26 % 0.48 % 0.02 % C3H8N3O 4.62 % 0.29 % 0.01 % C3H10N4 4.98 % 0.10 % 0.00 % C4H6O3 4.68 % 0.70 % 0.03 % C4H8NO2 5.04 % 0.51 % 0.02 % C4H10N2O 5.40 % 0.32 % 0.01 % C4H12N3 5.76 % 0.14 % 0.00 % C5H10O2 5.82 % 0.55 % 0.03 % C5H12NO 6.18 % 0.36 % 0.01 % C5H14N2 6.54 % 0.18 % 0.00 % C6H14O 6.96 % 0.41 % 0.02 % C8H6 9.05 % 0.36 % 0.01 %
质谱图中获得M+1/M与M+2/M的值分别为5.80%和0.50%,则通过比对可以确定C5H10O2为最可能的分子式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 beynon_dict = { "12" : { "C" : 12.0 }, "13" : { "CH" : 13.0078 }, "14" : { "N" : 14.0031 , "CH2" : 14.0157 }, . . . "250" : { "C11H26N2O4" : 250.1894 , "C12H14N2O4" : 250.0954 , "C12H16N3O3" : 250.1193 , ... "C18H18O" : 250.1358 , "C18H20N" : 250.1597 , "C18H34" : 250.2662 , "C19H22" : 250.1722 }
这样,针对某个质量数,通过遍历该质量数下所有分子,可以进行计算:
1 2 for k in beynon_dict.get(mass_num).keys(): calc(*decode_formula(k))
这样,一个简单的查询功能就完成了。