深入理解主成分分析 PCA

主成分分析（Principal Component Analysis，PCA）是一种统计分析方法，用于降低数据维数、简化数据集、提取数据特征。 PCA 的核心思想在于将数据变换到正交坐标系中，拆分为各坐标轴上的投影（即“成分”）的组合，并保留方差最大的几个成分（即“主成分”），以在数据维数降低的同时保留有效信息。

为了使读者全面、深入了解 PCA ，本文将从公式推导开始，阐明 PCA 的底层原理，并结合实例给出 PCA 的程序实现。

读者只需要最基本的线性代数知识即可阅读本文。

1 公式推导

1.1 问题引入

对于N维数据集D：

$$D=\begin{bmatrix} \mathbf{d}_1 & \mathbf{d}_2 & \cdots & \mathbf{d}_n \end{bmatrix}_{N\times n}$$

用列向量 $\mathbf{d_i}={\begin{pmatrix}x_i & y_i & z_i &...\end{pmatrix}^{\mathrm T}}_{N\times 1}$ 表示第 i 个数据点（共 n 个），用 $\mathbf{\bar{d}}=\frac1N{\begin{pmatrix}\sum x_i & \sum y_i & \sum z_i & ...\end{pmatrix}^{\mathrm T}}_{N\times 1}$ 表示数据的均值。

主成分分析实现降维是通过保留方差最大的几个主成分实现的。我们以单位向量

$$\mathbf{v_k} =\begin{bmatrix}\hat{i}_k\\\hat{j}_k\\\vdots\end{bmatrix}_{N\times 1}$$

来表示第 k 个坐标轴，那么首先要找到第一个主成分所对应的坐标轴 $\mathbf{v_1}$，也即数据中方差最大的方向。数据沿某个单位向量 $\mathbf{v}$ 的方差（即数据点投影到该向量所在直线上所得投影点的方差）可由下式求得（为简化表达，便于理解，采用方差的有偏估计，详见3.2节）：

$$\mathrm{var}(\mathbf{v})=\frac1n\sum_{i=1}^{n}||(\mathbf{d_i}-\mathbf{\bar{d}})^{\mathrm T}\mathbf{v}||^2\qquad（1）$$

上式为严谨的数学表达，$||\mathbf{z}||=\sqrt{\mathbf{z^T}\mathbf{z}}$ 表示向量 $\mathbf{z}$ 的长度（向量的模）。用简明的语言将上式表述如下：使数据点均值为 0，然后与单位向量作点积以投影到单位向量所在的方向上，得到一个 1x1 向量，即一个数，求这些数的方差。

我们期望求解使方差最大的向量，即

$$\mathbf{v_1}=\underset{\mathbf{v}}{\mathrm{argmax} }\ \mathrm{var}(\mathbf{v})$$

这是一个极值问题，我们需要对（1）式作进一步展开以探究方差与待求向量间的关系。

将（1）式展开如下：

$$\begin{aligned}\mathrm{var}(\mathbf{v}) & = \frac1n\sum_{i=1}^{n}||(\mathbf{d_i}-\mathbf{\bar{d}})^{\mathrm T}\mathbf{v}||^2\\&=\frac1n\sum_{i=1}^{n}\left(\sqrt{\mathbf{v}^\mathrm{T}(\mathbf{d_i}-\mathbf{\bar{d}})(\mathbf{d_i}-\mathbf{\bar{d}})^\mathrm{T}\mathbf{v}}\right)^2\\&=\frac1n\sum_{i=1}^{n}\mathbf{v}^\mathrm{T}(\mathbf{d_i}-\mathbf{\bar{d}})(\mathbf{d_i}-\mathbf{\bar{d}})^\mathrm{T}\mathbf{v}\\&=\mathbf{v}^\mathrm{T}\left(\frac1n\sum_{i=1}^{n}(\mathbf{d_i}-\mathbf{\bar{d}})(\mathbf{d_i}-\mathbf{\bar{d}})^\mathrm{T}\right)\mathbf{v}\\&=\mathbf{v}^\mathrm{T}\Sigma \mathbf{v}\end{aligned}\qquad(2)$$

其中，$\Sigma$ 称为协方差矩阵：

$$\Sigma=\frac1n\sum_{i=1}^{n}(\mathbf{d_i}-\mathbf{\bar{d}})(\mathbf{d_i}-\mathbf{\bar{d}})^\mathrm{T}\qquad(3)$$

1.2 协方差矩阵

为了进一步了解协方差矩阵的意义以及求法，我们将其展开（以二维数据为例，并将数据去中心化使其均值为 0，便于计算）：

$$\begin{aligned}\Sigma & = \frac1n\sum_{i = 1}^{n}\mathbf {d_i}\mathbf{d_i}^\mathrm{T}\\&= \frac1n\sum_{i = 1}^{n}\begin{bmatrix} x_i^2 & x_iy_i \\ y_ix_i & y_i^2 \\\end{bmatrix}\\&=\begin{bmatrix} \frac1n\sum_{i = 1}^{n} x_i^2 & \frac1n\sum_{i = 1}^{n}x_iy_i \\ \frac1n\sum_{i = 1}^{n}y_ix_i & \frac1n\sum_{i = 1}^{n}y_i^2 \end{bmatrix}\\&=\begin{bmatrix}cov(x,x) & cov(x,y)\\ cov(y,x) & cov(y,y)\end{bmatrix} \end{aligned}\qquad(4)$$

从上式中，我们了解到协方差矩阵是一个 N 维方阵，方阵的对角线上为各维数据的方差，并定义了协方差：

$$cov(a,b)=\frac{\sum_{i=1}^{n}a_ib_i}n \qquad(5)$$

协方差表示两个变量的相关性强弱。当协方差大于 0 时，a 和 b 同向变化，呈正相关关系，反之则为负相关关系，且协方差绝对值越大，相关性越强。当协方差等于 0 时，代表两个变量无相关性。

变量与自身的协方差即为方差，而交换变量的位置，不改变它们的协方差，即协方差矩阵不仅是方阵，还是对称阵：

$$\begin{aligned}\Sigma &=\begin{bmatrix}cov(x,x) & cov(x,y)\\ cov(x,y) & cov(y,y)\end{bmatrix}\end{aligned}\qquad(6)$$

协方差矩阵可以由去中心化的数据经矩阵乘积运算得到：

$$\begin{aligned}\Sigma &=\begin{bmatrix} \frac1n\sum_{i = 1}^{n} x_i^2 & \frac1n \sum_{i = 1}^{n}x_iy_i \\ \frac1n\sum_{i = 1}^{n}y_ix_i & \frac1n\sum_{i = 1}^{n}y_i^2 \end{bmatrix} \\&=\frac1n\begin{bmatrix} x_1 & x_2 & ... & x_n \\ y_1 & y_2 & ... & y_n \end{bmatrix}\begin{bmatrix} x_1 & y_1\\ x_2 & y_2 \\ \vdots & \vdots\\x_n & y_n\end{bmatrix}\\&=\frac1nDD^{\mathrm{T}}\end{aligned}\qquad(7)$$

在了解了协方差矩阵的相关知识后，我们可以进一步探究如何求 $\underset{\mathbf{v}}{\mathrm{argmax} }\ \mathrm{var}(\mathbf{v})$ 了。

1.3 极值求解

如何求函数的极值？我们首先想到的就是导数。当导数为 0 时，函数可能取到极值。但在这里，$\mathrm{var}(\mathbf{v})=\mathbf{v}^\mathrm{T}\Sigma \mathbf{v}$ 的自变量 $\mathbf{v}$ 是一个向量（一维矩阵），如果读者掌握泛函分析相关知识，则容易理解 $\mathbf{v}^\mathrm{T}\Sigma \mathbf{v}$ 对 $\mathbf{v}$ 的求导（见3.3节）。为便于理解，我们将 $\mathrm{var}(\mathbf{v})$ 作为多元函数处理，将 $\mathrm{var}(\mathbf{v})$ 的极值问题转化为多元函数的极值问题（用线性代数的语言来讲，$\mathrm{var}(\mathbf{v})$ 是一个二次型矩阵，而二次型对应着二次函数）。

已知

$$\mathbf{v} =\begin{bmatrix}\hat {i} \\ \hat {j} \end{bmatrix}\qquad \Sigma =\begin{bmatrix}cov(x,x) & cov(x,y)\\ cov(x,y) & cov(y,y)\end{bmatrix}$$

将 $\mathrm{var}(\mathbf{v})$ 表达为以 $\hat{i}$ 和 $\hat{j}$ 为自变量的形式：

$$\begin{aligned}\mathrm{var}(\mathbf{v}) & = \mathbf{v}^\mathrm{T}\Sigma \mathbf{v} \\&=\begin{bmatrix}\hat {i} &\hat {j}\end{bmatrix}\begin{bmatrix}cov(x,x) & cov(x,y)\\ cov(x,y) & cov(y,y)\end{bmatrix}\begin{bmatrix}\hat {i} \\\hat {j}\end{bmatrix}\\\mathrm{var}({\hat{i}},{\hat{j}})&=cov(x,x){\hat{i}}^2+2cov(x,y){\hat{i}}{\hat{j}}+cov(y,y){\hat{j}}^2\qquad(8)\end{aligned}$$

在将 $\mathrm{var}(\mathbf{v})$ 转化为二次函数后，可以利用拉格朗日乘子法，将极值问题转化为含两个变量（即 $\hat{i}$ 和 $\hat {j}$，协方差矩阵是已知的）和一个约束条件（即 ${\hat{i}}^2+{\hat{j}}^2-1=0$）的方程组的解的问题。

构造如下的函数 $F$：

$$\begin{aligned}F({\hat{i}},{\hat{j}},\lambda)&=\mathrm{var}({\hat{i}},{\hat{j}})-\lambda({\hat{i}}^2+{\hat{j}}^2-1)\\&=cov(x,x){\hat{i}}^2+2cov(x,y){\hat{i}}{\hat{j}}+cov(y,y){\hat{j}}^2\\&{\quad}-\lambda({\hat{i}}^2+{\hat{j}}^2-1)\end{aligned}\qquad(9)$$

其中 $\lambda$ 是拉格朗日乘子。当 $F$ 对所有自变量的偏导数为 0 时，可取到所有极值点：

$$\left\{\begin{aligned}\frac{\partial F}{\partial {\hat{i}}} & = 2cov(x,x) {\hat{i}}+2cov(x,y) {\hat{j}}-2{\lambda\hat{i}} = 0\\ \frac{\partial F}{\partial {\hat{j}}} & = 2cov(x,y) {\hat{i}}+2cov(y,y) {\hat{j}}-2{\lambda\hat{j}} = 0\\ \frac{\partial F}{\partial {\lambda}} & = {\hat{i}}^2+{\hat{j}}^2-1 =0 \quad (s.t.)\end{aligned}\right.\qquad(10)$$

以上三个方程组成的方程组，最后一个为约束条件（$s.t.$=subject to），将前两个方程含 $\lambda$ 的部分移到等号右侧并写成矩阵乘积的形式，我们惊奇地发现，当$\mathrm{var}(\mathbf{v})$ 取得极值时，$\lambda$ 就是协方差矩阵的特征值，而 $\mathbf{v}$ 则为该特征值对应的特征向量！

$$\begin{array}{c}\left\{ \begin{aligned} 2cov(x,x) {\hat{i}}+2cov(x,y) {\hat{j}}&=2{\lambda\hat{i}}\\ 2cov(x,y) {\hat{i}}+2cov(y,y) {\hat{j}}&=2{\lambda\hat{j}} \end{aligned}\right.\\ \downarrow \\\begin{bmatrix}cov(x,x) & cov(x,y)\\ cov(x,y) & cov(y,y)\end{bmatrix}\begin{bmatrix}\hat {i} \\\hat {j}\end{bmatrix}=\lambda\begin{bmatrix}\hat {i} \\\hat {j}\end{bmatrix}\\\end{array}$$

即：

$$\Sigma\mathbf{v}=\lambda \mathbf{v}\qquad(11)$$

经过上述的求解过程，我们不仅求出了使 $\mathrm{var}(\mathbf{v})$ 取得最大值时的单位向量（即最大特征值对应的特征向量），事实上还求出了所有使 $\mathrm{var}(\mathbf{v})$ 取得极值的向量。根据特征向量的性质，这些向量相互正交（在欧氏空间中，这些正交的单位向量称为标准正交基，它们组成一个正交坐标系），将向量按特征值从大到小排序，它们分别代表数据中最大方差和次大方差的方向，对应着第一和第二主成分。对于多维数据，也可以根据类似解法得到 $\Sigma\mathbf{v}=\lambda \mathbf{v}$ 之结论。

1.4 数据降维与重构

对于一个 N 维且各维度间线性不相关的数据集，可得到 N 个特征向量，N 个主成分。如果数据冗余度较高，则仅有少数几个特征值较大，而其余的特征值接近于 0，我们可以根据特征值较大的一组特征向量（一组标准正交基）定义一个比原始数据维度低得多的子空间，并将原始数据投影到子空间上，实现数据降维。

如果取前 M 个特征向量（M ≤ N） 组成矩阵：

$$\begin{aligned}V & = \begin{bmatrix}\bf{v_1} & \bf{v_2} &...&\bf{v_M} \end{bmatrix}\\&=\begin{bmatrix}\hat{i}_1 & \hat{i}_2 & \cdots & \hat{i}_M\\\hat{j}_1 & \hat{j}_2 & \cdots & \hat{j}_M\\ \vdots & \vdots & \ddots & \end{bmatrix}_{N\times M}\end{aligned}\qquad(12)$$

将去中心化的原始数据与该矩阵的转置乘积，即得降维后的数据集（注意，该步之后的所有数据均去中心化。去中心化过程可逆，不影响数据重构）：

$$D'_{M\times n}={V^{\mathrm T}}_{M\times N} D_{N\times n}\qquad(13)$$

求新数据集的协方差矩阵：

$$\begin{aligned}\Sigma'& = \frac1n{D'}D'^{\mathrm T}\\ & = \frac1nV^{\mathrm T}{D}{D}^{\mathrm T}V\\ & = V^{\mathrm T}\Sigma V\\ & = \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_M\end{bmatrix}_{M\times M}\end{aligned}\qquad(14)$$

由于 $V$ 是 $\Sigma$ 的各特征向量组成的矩阵，因此 $\Sigma'$ 为对角矩阵，对角线上的元素为特征值。这意味着，降维去除了数据各维度间的相关性。同时，(14) 式也反映了 $\lambda$ 值与数据在各主成分中分散程度的关系。

当且仅当 M = N 时，数据不降维而仅进行了去相关化，不丢失任何信息。去相关化是数据标准化流程之一。

注意到由于 V 中各向量相互正交，所以当且仅当 M = N 时（V 为方阵时）有 $V^{\mathrm T}=V^{-1}$，这意味着协方差矩阵 $\Sigma'$ 可以写成 $\Sigma'=V^{-1}\Sigma V$ 的形式，而该变换恰好对应着二次型的标准化，也相当于对原始数据的协方差矩阵 $\Sigma$ 进行特征值分解，将协方差矩阵所代表的线性变换分解为旋转变换和缩放变换两个部分。

可以用（15）式由降维后的数据重构出输入数据，但当 M < N 时，重构出的数据和原始数据会有一定差异，差异的大小与选择的主成分个数以及这些主成分对应特征值大小有关。

$$\begin{aligned} D''_{N\times n} &=V_{N\times M}D'_{M\times n} \\& = V_{N\times M}{V^{\mathrm{T}}}_{M\times N}{D^{\mathrm{T}}}_{N\times n} \\& = V_{N\times M}{V^{\mathrm{-1}}}_{M\times N}{D^{\mathrm{T}}}_{N\times n} \end{aligned}\qquad(15)$$

若将（15）式理解为原始数据的两次旋转变换，将更有助于理解 PCA 的几何意义：第一次旋转变换将数据变换到新坐标系中，实现了去相关化（当 M < N 时还实现了降维），第二次旋转变换为第一次的逆操作，它将处理后的数据在原始坐标系中表示，实现了数据重构。

1.5 PCA 与 SVD 的关系

奇异值分解（Singular Value Decomposition，SVD）是一种重要的矩阵分解方法，对于实数域和复数域的任意 m × n 阶矩阵，都可以通过奇异值分解使得：

$$D_{m\times n}=U_{m\times m}S_{m\times n} {V^{\mathrm{T}}}_{n\times n}\qquad(16)$$

其中，其中 $U$ 是 m × m 阶酉矩阵（若 $D$ 为实矩阵，则 $U$ 为正交矩阵，下同），$S$ 是 m × n 阶对角矩阵，${V^{\mathrm{T}}}$ 是 n × n 阶酉矩阵。$U$ 和 ${V^{\mathrm{T}}}$ 中的向量分别称为左奇异向量和右奇异向量，$S$ 中对角线上的元素 $\sigma$ 称为奇异值，按降序排列。

为什么 SVD 可用来进行 PCA ？我们通过 SVD 中三个矩阵的求解过程来看：

$$\begin{aligned}DD^{\mathrm{T}} & = US{V}(US{V})^{\mathrm{T}}\\&=US{V}V^{\mathrm{T}}S U^{\mathrm{T}}\\&=US^2 U^{\mathrm{T}}\end{aligned}\qquad(17)$$

$$\begin{aligned}D^{\mathrm{T}}D & = (US{V})^{\mathrm{T}}US{V}\\&=V^{\mathrm{T}}S U^{\mathrm{T}}US{V}\\&=VS^2 V^{\mathrm{T}}\end{aligned}\qquad(18)$$

变换后即得：

$$\begin{aligned}DD^{\mathrm{T}}U & = S^2U \qquad(19)\\D^{\mathrm{T}}DV&=S^2V\qquad(20)\end{aligned}$$

即 $U$ 是 $DD^{\mathrm{T}}$ 的特征向量组成的矩阵，$V$ 是 $D^{\mathrm{T}}D$ 的特征向量组成的矩阵，$U$ 和 $V$ 具有相同的特征值。

结合（19）（11）（7）三式，我们发现 PCA 和 SVD 都在求 $DD^{\mathrm{T}}$ 的特征向量，如果矩阵每列代表一个数据点，则 PCA 中特征向量组成的矩阵其实就是奇异值分解中的 $U$ 矩阵，这也解释了 SVD 为何也能求解 PCA 的问题（如果认为矩阵每行代表一个数据点，则这时 SVD 的 $V$ 矩阵对应 PCA 中特征向量组成的矩阵，因此应多加注意矩阵行列的含义）。

怎样理解 PCA 与 SVD 的关系？

• 从目的来看，PCA 是为了将数据降维，提取主要特征，而 SVD 是线性代数中一种矩阵分解手段，属于底层的线性代数方法，其与 PCA 中所用到的特征值分解同级。
• 从算法来看，PCA 中协方差矩阵的运算量大，而某些 SVD 迭代求解算法不需要求解协方差矩阵就能得出结果，能够极大提升程序运行效率，因此在科学计算中，PCA 的底层都是用 SVD 实现的。

对于 SVD 的其他问题，如奇异值与特征值的关系，以及 SVD 最佳近似的选择等问题，出于篇幅原因，本文不再讨论。

2 程序实现

2.1 生成数据

首先，利用随机数生成二维数据集D，D的每一列对应一个数据点：

np.random.seed(100) # 为随机数种子赋定值，便于重复结果
D = np.zeros((2,10)) # 新建一个2行，10列的矩阵，并把第一行当作x坐标，第二行为y坐标
D[:1,:]=np.random.uniform(1,10,(1,10)) # 为矩阵第一行赋随机数值，最小值为1，最大值为10
D[1:,:] = 0.5*D[:1,:]+np.random.uniform(-2,2,(1,10))# 为矩阵第二行赋值，0.5倍的第一行加上最小值为-2，最大值为2的随机数，使得x，y坐标在各自具有随机性的同时，x和y有一定相关关系

对数据进行去中心化，使得数据均值为 0：

D_norm = D-D.mean(axis=1).reshape(-1,1)# 求每一行的平均值，并转换成列向量以进行元素运算

2.2 计算主成分

利用numpy.cov计算协方差矩阵Σ：

Sigma = np.cov(D_norm) 

$$\Sigma=\begin{bmatrix}7.2366  & 2.5111\\2.5111  &2.7329\end{bmatrix}$$

利用numpy.linalg.eig计算协方差矩阵的特征值和特征向量，并将特征向量按照特征值从大到小排序：

#计算特征向量和特征值
eigvals,V  = np.linalg.eig(Sigma)
#按照特征值从大到小重新排序
V = V[:,np.argsort(-eigvals)]
eigvals = eigvals[np.argsort(-eigvals)]

V即特征向量构成的矩阵：

$$V=\begin{bmatrix}0.9131  &  -0.4077\\0.4077  & 0.9131\end{bmatrix}$$

eigvals为每个特征向量对应的特征值：

$$eigvals=\begin{pmatrix}8.3576&1.6119\end{pmatrix}$$

2.3 PCA 的可视化

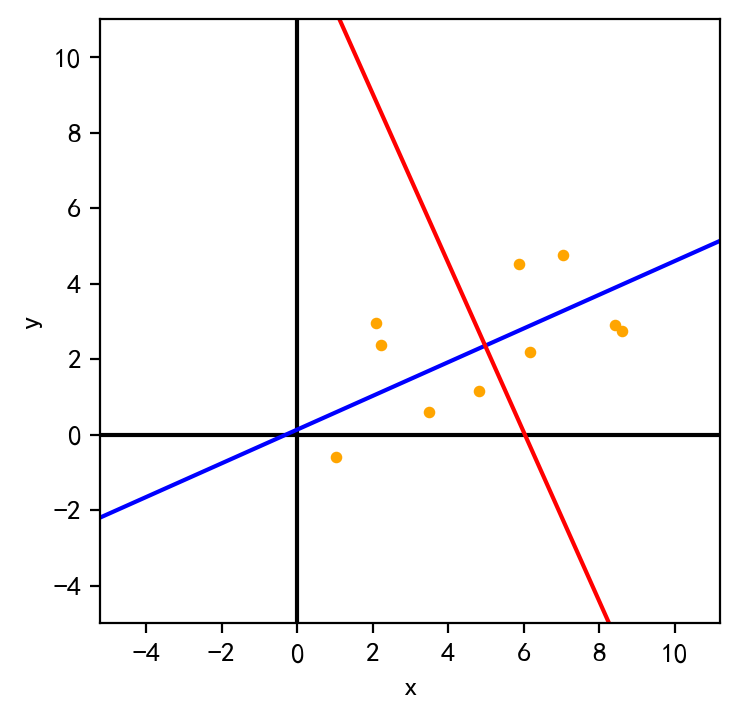
将特征向量所在直线（过原点）根据原始数据均值进行位移，画出新的坐标系

fig=plt.figure(100,figsize=(4,4),dpi=200)
ax=fig.gca()
plt.axis('equal') # 使坐标轴尺度相同
size=9
ax1=np.array([-V[:,0],V[:,0]])*2*size+D.mean(axis=1)# 第一主成分所在直线
ax2=np.array([-V[:,1],V[:,1]])*2*size+D.mean(axis=1) # 第二主成分所在直线
ax.scatter(D[0],D[1],label='origin',s=10,c='orange') 
ax.set(xlim=(-5,11),ylim=(-5,11),xlabel='x',ylabel='y',xticks=range(-4,12,2))
ax.axvline(0,c='black') # x轴
ax.axhline(0,c='black') # y轴
ax.plot(ax1[:,0],ax1[:,1],c='blue')
ax.plot(ax2[:,0],ax2[:,1],c='red')

从图中可明显看出，数据在蓝色轴上的方差最大。

取数据的第一主成分，即将数据与最大特征值对应的特征向量作点积：

V[:,0:1].T @ D_norm # 必须用去中心化的数据

输出结果如下：

array([[ 1.7061, -2.0705, -0.6403,  3.459 , -4.8043, -2.3921,  2.8564,
         3.3724, -2.5048,  1.0181]])

由于只保留一个主成分，因此降维后的数据变成了一维向量。

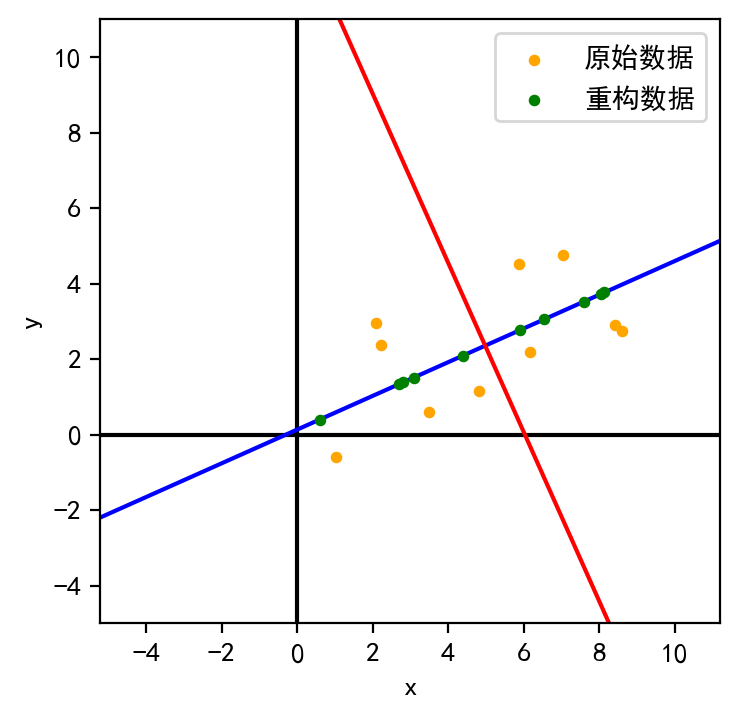
为了可视化降维的效果，根据第一主成分重构数据并将其可视化：

D_recover=V[:,0:1] @ V[:,0:1].T @ D_norm + D.mean(axis=1).reshape(-1,1)

可见，重构后的数据落在了第一主成分所在的轴上。

2.4 PCA 的标准库函数实现

• 使用sklearn.decomposition.PCA

from sklearn.decomposition import PCA 
pca =  PCA(n_components=1)# 建立模型，选定保留的维数
pca.fit_transform(D.T) #用数据拟合模型并对进行降维处理。注意该函数输入矩阵中每个数据点用行向量表示

array([[-1.7061],
       [ 2.0705],
       [ 0.6403],
       [-3.459 ],
       [ 4.8043],
       [ 2.3921],
       [-2.8564],
       [-3.3724],
       [ 2.5048],
       [-1.0181]])

使用pca.components_.T输出主成分对应的特征向量：

array([[-0.9131],
       [-0.4077]])

虽然输出向量我们自己算出的向量只是方向相反，因此不影响 PCA 的结果。

使用pca.inverse_transform重构数据（略）

• 使用numpy.linalg.svd（奇异值分解 SVD，见1.5节）

如前文所述，对于用列向量表示一个数据点的数据集D，使用奇异值分解得到的U，S，Vt三个矩阵，其中U恰好是 PCA 中的全部特征向量构成的矩阵：

U,S,Vt = np.linalg.svd(D_norm)
print('U=\n',U)

U=
 [[-0.9131 -0.4077]
 [-0.4077  0.9131]]

只要知道特征向量，就能进行降维，因此后续实现过程不再赘述。

2.5 PCA 实例

注：本实例来源于此书（视频链接），代码有删改。

卵巢癌（ovarian cancer）指生长在卵巢上的恶性肿瘤，其早期诊断困难，发病率虽较低但死亡率居于妇科癌症首位，严重威胁女性健康。如果能够通过各种指标对卵巢癌进行预测，将对其诊疗非常有益。

能否通过 PCA 发现卵巢癌患者与正常人的指标差异？现采集了 216 名试验者的 4000 个指标，其中 121 名为患者，其余 95 名正常。指标数据按每人一行存储在ovariancancer_obs.csv当中，标签数据（是否患癌）储存在ovariancancer_grp.csv当中。

首先，读取指标数据并赋给obs变量（numpy.ndarray)，读取标签数据并赋给grp变量（list)：

# 导入依赖库
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# 读取文件
obs = np.loadtxt('ovariancancer_obs.csv',delimiter=',')
with open('ovariancancer_grp.csv') as fp:
    grp = fp.read().split('\n')
# 输出结果
print('obs:',obs.shape,type(obs),'\n',obs)
print('\ngrp:',len(grp),type(grp),'\n',grp)

obs: (216, 4000) <class 'numpy.ndarray'>
 [[ 0.0639  0.0332  0.0185 ...  0.0388  0.0382  0.0321]
 [ 0.0254  0.0511  0.0563 ...  0.0204  0.0233  0.02  ]
 [ 0.0255  0.0361  0.0542 ... -0.0094  0.0215  0.0256]
 ...
 [ 0.0236  0.0213  0.0162 ...  0.0083  0.0047  0.0248]
 [ 0.0284  0.0233  0.0046 ...  0.01    0.0174  0.0315]
 [ 0.0274  0.027   0.0153 ...  0.0266  0.0277  0.0404]]

grp: 216 <class 'list'>
 ['Cancer', 'Cancer', 'Cancer', ... , 'Normal', 'Normal', 'Normal']

对指标数据进行 SVD（这里使用的参数full_matrices=False代表对矩阵进行精简分解，由于在 $S$ 矩阵中具有很多零值，因此会在计算 $D=US{V^{\mathrm{T}}}$ 时进行很多无用的计算，即 $S$ 中的零值以及 $U$ 和 $V$ 中的一些行或列可以删除且不会影响分解的准确性，并且还能节省计算时间与存储空间）：

U, S, Vt = np.linalg.svd(obs,full_matrices=False)
print(U.shape,S.shape,Vt.shape)

(216, 216) (216,) (216, 4000)

在分解之后得到的“精简矩阵”的形状如上所示。如果不使用精简分解，则 ${V^{\mathrm{T}}}$ 矩阵的形状应为(4000, 4000)，但在降维时只有前 216 行是有用的，因此只保留前 216 行。

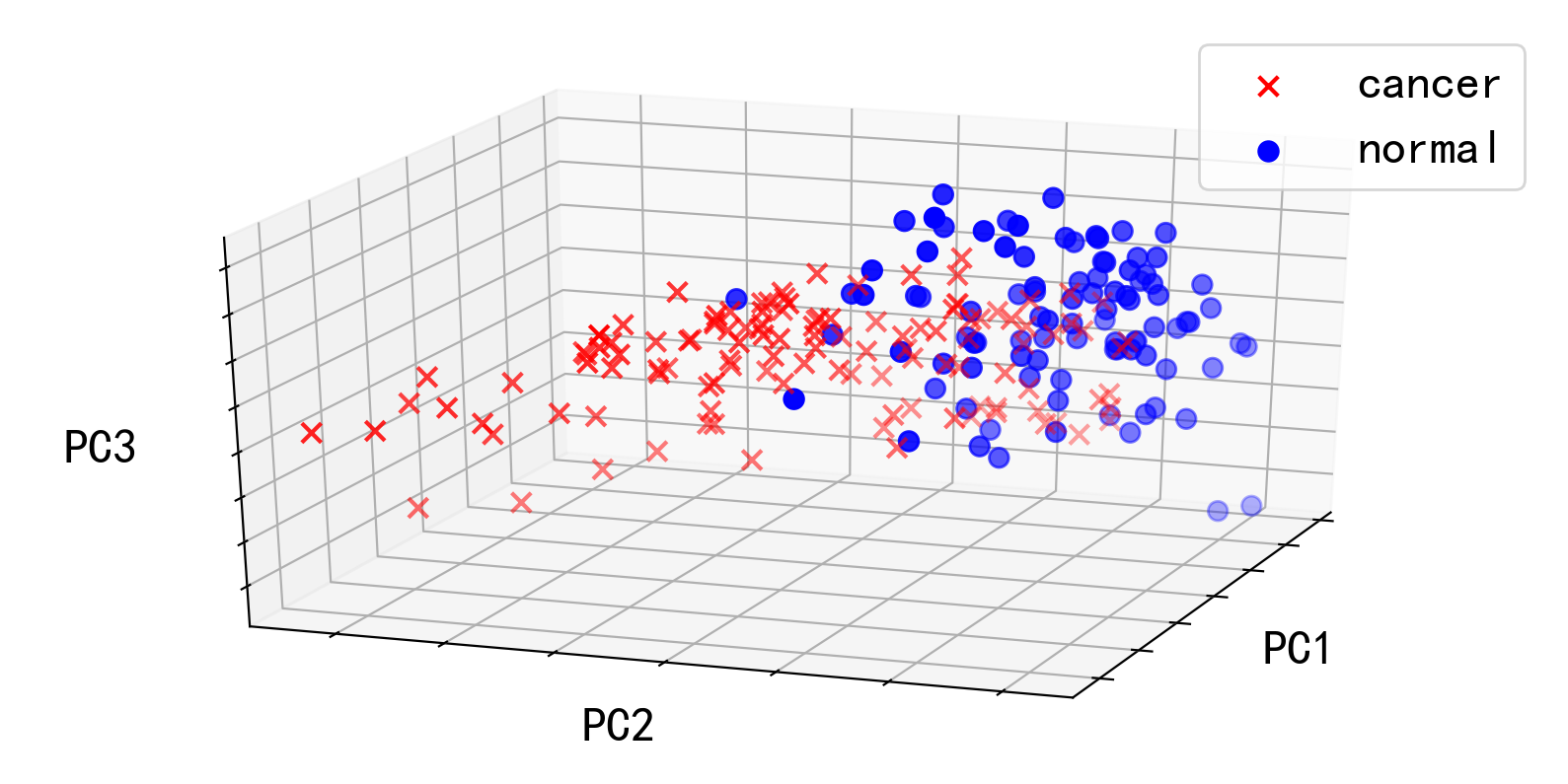
我们提取前 3 个主成分，并将其在三维空间中可视化：

components = obs @ Vt[:3,:].T # 对于行向量表示的数据点，V为特征向量组成的矩阵，由DV降维
cancer_index=[i for i in range(len(grp)) if grp[i] == 'Cancer'] # 提取患者索引
normal_index=[i for i in range(len(grp)) if grp[i] == 'Normal'] # 提取正常索引
components_cancer=components[cancer_index,:] # 分离患癌和正常的主成分（在散点图中区分）
components_normal=components[normal_index,:]

fig1 = plt.figure(figsize=[10,5],dpi=200)
plt.axis('equal') 
plt.rcParams.update({'font.size': 18})
ax = fig1.add_subplot(111, projection='3d')
ax.scatter(*components_cancer.T,marker='x',color='r',s=50,label='cancer')
ax.scatter(*components_normal.T,marker='o',color='b',s=50,label='normal')
ax.view_init(25,20)
ax.set(xlabel='PC1',ylabel='PC2',zlabel='PC3',xticklabels=[],yticklabels=[],zticklabels=[])
ax.legend()
plt.show()

可见，在三个主成分对应的基向量所张成的空间中，患者和正常人在主成分的空间分布上有明显的差别，这意味我们成功地从 4000 个指标中用 3 个维度提取出了患者与正常人的差异之处。

3 讨论与补充

3.1 PCA 的缺点与改进

• PCA 对变量缩放敏感。如果原始数据的不同维度所表达的意义不同或尺度相差太大，则需要先对数据进行标准化处理，使得数据各维度的均值为0，标准差为1（即服从高斯分布）。

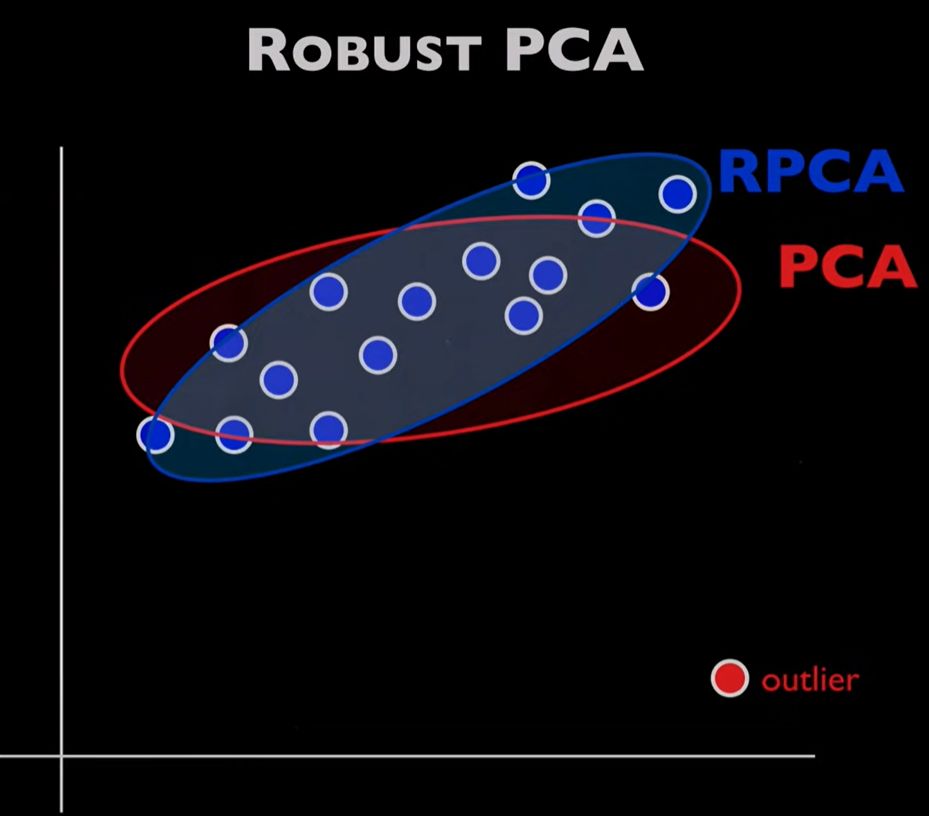
• PCA 对离群值敏感。大噪声和少量离群值可以显著改变 PCA 的结果（见下图）。鲁棒主成分分析（Robust Principal Component Analysis，RPCA）可以改善 PCA 在大噪声或严重离群点条件下的表现。

  PCA受离群值影响很大，而RPCA可以将离群值分离出来。图源

  RPCA 假设原始矩阵可以表示为一个低秩矩阵（L，low rank=低秩）和一个稀疏矩阵（S，Sparse=稀疏）的叠加：

  $$M=L+S$$

  其中低秩矩阵表示数据所包含的真实信息，稀疏矩阵则代表数据中的噪声。噪声的存在使得 PCA 的降维效果不理想，而RPCA 则通过将数据中的噪声分离出来解决这一问题。

  RPCA 的算法和实现将在后文详述。

• PCA 不能有效分离信息。 PCA 只能压缩数据，提取数据的特征，而不能分离信息源。因此，在信号处理中，不能通过 PCA 分离出独立的信号源。独立成分分析（Independent components analysis，ICA）可以将数据或信号 $s$ 分解为独立的、非高斯的信号源的线性组合 $x$：

  $$s=Wx$$

  其中矩阵 $W$ 称为解混矩阵，本文不讨论该矩阵的解法。 PCA 和 ICA 的组合在脑科学领域有广泛的应用。

3.2 关于方差的有偏和无偏估计

上文中，为了简化公式，便于理解，使用了

$$\sigma^2=\frac1n\sum\limits^n_{i=1}\left(X_i-\bar X\right)^2$$

表示随机变量 $X$ 的方差，这在 $X$的数学期望 $\mu$ 是已知的情况下是成立的。当 $X$ 的数学期望 $\mu$ 未知，而又使用 $\bar X$ 估计 $\mu$ 时，会倾向于低估方差。我们称这种估计方差的方法为有偏估计。

严谨的数学证明告诉我们，在的数学期望 $\mu$ 未知的情况下，样本方差的无偏估计为下式：

$$\sigma_{unbiased}^2=\frac1{n-1}\sum\limits^n_{i=1}\left(X_i-\bar X\right)^2$$

即将分母中的 n 替换为 n - 1。现实中的数据方差估计多采用无偏估计，科学计算工具包中方差的计算（如numpy.cov）默认也采用无偏估计。

由于有偏估计和无偏估计的方差是一个等比例缩放的关系，因此采用有偏估计不会改变主成分分析的特征向量。

3.3 关于矩阵对矩阵求导

有以下矩阵求导公式：

$$\frac{\partial x^{\mathrm T}Ax}{\partial x}=(A+A^{\mathrm T})x\qquad(S1)$$

如果$A=A^{\mathrm T}$，则有

$$\frac{\partial x^{\mathrm T}Ax}{\partial x}=2Ax\qquad(S2)$$

如果$A=I$，即A为单位矩阵，则有：

$$\frac{\partial x^{\mathrm T}Ix}{\partial x}=\frac{\partial x^{\mathrm T}x}{\partial x}=2x\qquad(S3)$$

将（9）式写为矩阵运算的形式：

$$F(\mathbf{v},\lambda )=\mathbf{v}^\mathrm{T}\Sigma \mathbf{v}-\lambda (\mathbf{v}^\mathrm{T}\mathbf{v}-1)\qquad(S4)$$

求 $F$ 的偏导数，并按照 $S2$、$S3$ 两式进行化简：

$$\left\{\begin{aligned}\frac{\partial F}{\partial \mathbf{v}}&=2\Sigma \mathbf{v}-2\lambda \mathbf{v}=0\\\frac{\partial F}{\partial \lambda}&=\mathbf{v}^\mathrm{T}\mathbf{v}-1=0\quad(s.t.)\end{aligned}\right.\qquad(S5)$$

立即得：

$$\Sigma\mathbf{v}=\lambda \mathbf{v}\qquad(11)$$

4 参见

1. 知乎：如何直观地理解「协方差矩阵」？

2. 知乎：如何理解拉格朗日乘子法？

3. 知乎：为什么样本方差（sample variance）的分母是 n-1？

4. 知乎：如何理解矩阵对矩阵求导？

5. bilibili：什么是奇异值分解 SVD？ SVD 如何分解时空矩阵？

6. bilibili：用最直观的方式告诉你：什么是主成分分析 PCA

7. （英文）书籍及配套视频：数据的降维和变换 Dimensionality Reduction and Transforms

8. （英文）SVD 算法 Simple SVD algorithms

9. （英文）Youtube：Robust Principal Component Analysis (RPCA)

10. （英文）ICA 简介与算法 Independent Component Analysis (ICA)