1. 过电势的产生
电解过程是一个不可逆过程,电极上有电流通过时,随着不可逆程度的增加,电势值偏离可逆电势的程度也越来越大。我们将这种现象称为电极的极化。
我们在物理化学中已经学过,极化主要分为浓差极化、电化学极化和电阻极化。
- 浓差极化是由于电极表面反应物的浓度与本体溶液间存在差别导致电势值发生偏离,是传质扩散过程的影响。极谱分析法就是依据扩散速度与浓度的关系测量离子浓度的。
- 电化学极化则源于电极的电荷转移和氧化还原过程,反应需克服一定的势垒导致需要额外的能量才能使反应正向进行。
- 电阻极化是由于电极表面生成了导电性很差的物质。
在以上三种极化中,电阻极化由于其对超电势的影响较为简单,我们略去它;浓差极化虽然不能完全消除,但是可以通过搅拌增强传质作用,进而使浓差极化相对于电化学极化也可以忽略。因此我们可以认为在以上条件下,仅电化学极化对过电势有贡献。
在这种情况下我们建立一个电极反应的模型,通过探究电极电势和电流的关系,推导出三个电化学基本方程,深化大家对电化学的认识。
2. 模型的建立
我们继续建立电化学模型。首先我们需要搭建一个虚拟的电解池,这个装置由工作电极、对电极和含有一对氧化还原物质的电解质溶液组成。将电源两极与电极相连接,使电极电势发生变化,我们研究在工作电极及其周围发生的氧化还原过程。
Ox + ne− ⇌ Red
为了描述电极表面和溶液界面处的电势变化,我们还需要引入经典的Helmholtz双电层模型,
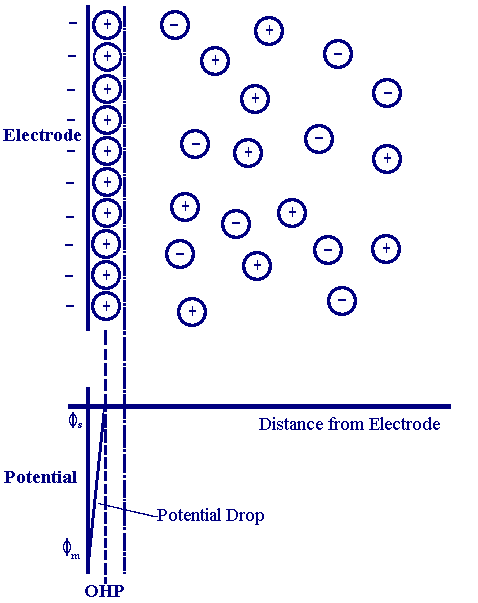 图1:Helmholtz双电层模型,描述了电极表面电势的变化。
图1:Helmholtz双电层模型,描述了电极表面电势的变化。
并假设电解质溶液的浓度足够大,使得电势的变化基本仅限于Helmholtz层内部,也就是说,当电极电势由E1变化为E2时,溶液本体的电势可近似看作不变,而金属电极上的电势变化了E2-E1.
为了定量表达电极反应过程,我们需要利用过渡态理论进行处理,认为反应经历活化络合物中间体,反应的活化能等于活化络合物中间体的化学势与反应物的化学势的差值。我们用反应坐标与势能关系图将反应过程画出来:
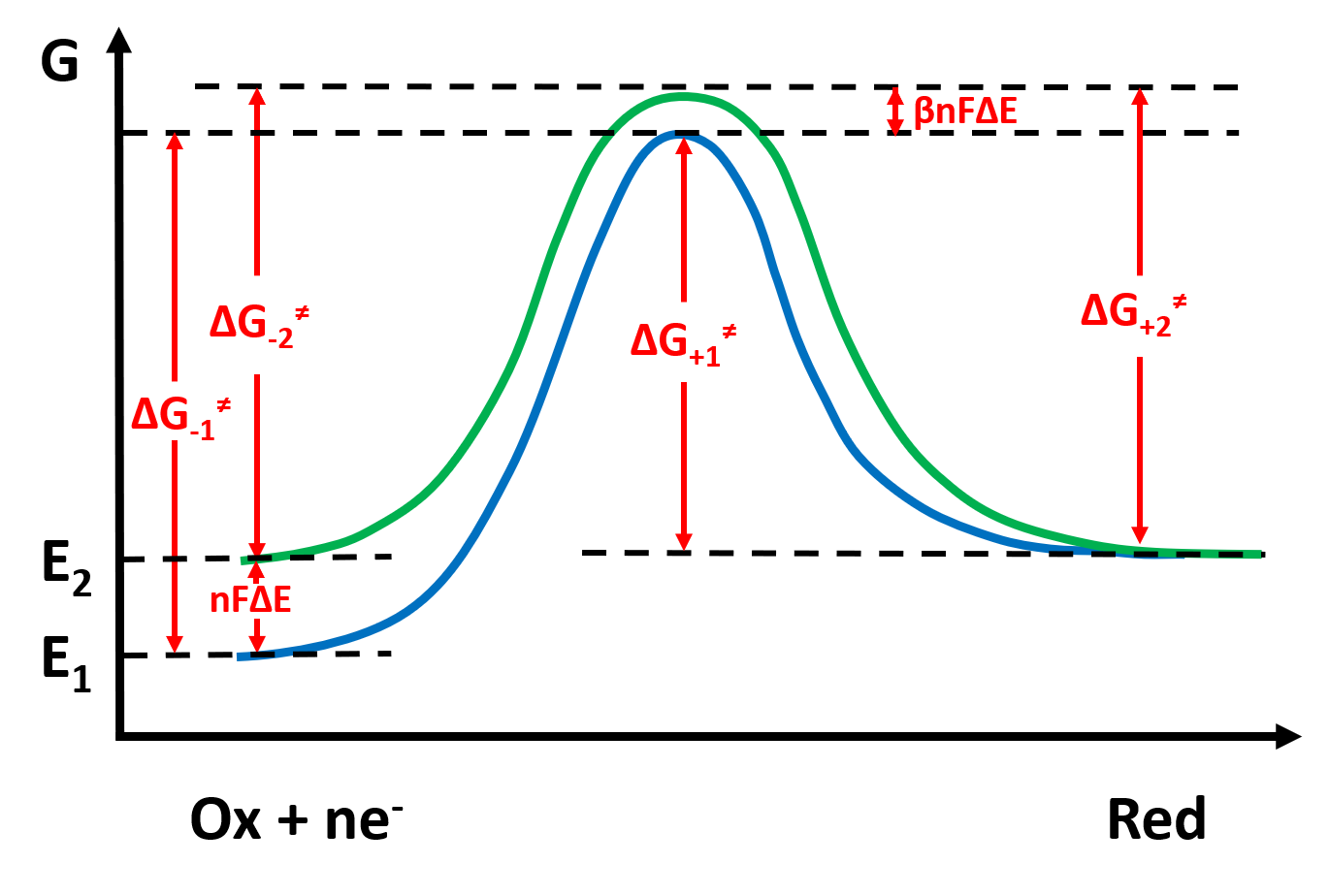 图2:在两个电极电势下的反应势能曲线
图2:在两个电极电势下的反应势能曲线
现在我们的模型建立完毕,总结一下:
- 理论基础:过渡态理论(刻画反应过程,计算反应速率)
- 电化学模型:双电层模型(描述电势的变化)
- 假设:电化学极化(过电势仅由电化学极化引起)、电解质溶液浓度大(使得电势的变化近似只发生于双电层附近)
现在我们终于可以进行一些理论推导了。
3. Nernst方程与B-V方程的推导
首先,我们假设该反应在电势E1下进行,则反应物 Ox + ne− 与活化络合物的化学势之差 ΔG−=(E1) 可以看作为还原反应的活化能,根据Arrhenius公式,得到还原反应的速率和电流密度:
v−(E1)j−(E1)=k−⋅cOx⋅exp(−RTΔG−=(E1))=−nFcOxk−exp(−RTΔG−=(E1))
当继续降低电极电势至E2时,反应物(氧化型)更易得到电子,因此还原反应的活化能会降低。那么活化能具体降低了多少呢?我们假设Ox和Red是在电势变化的界面区之外进行电子的得失的,也就是说,改变电极电势不会影响Ox和Red的化学势,而仅使得电极内部电子的化学势发生变化,并且对于1mol电子而言,其势能的变化值为 −nFΔE(势能升高,电子更易离开金属)。因此,如果改变电极电势会改变反应物中电子的化学势而不改变活化络合物的化学势,则正反应的活化能应当降低了 −nFΔE。但是,实际上,反应物化学势的变化不可能不会影响到活化络合物化学势的变化,活化络合物化学势也会升高 −βnFΔE (0<β<1),这就使得正反应(还原反应)的化学势降低值要小于 −nFΔE,而实际降低了 −(1−β)nFΔE,因此有
v−(E2)j−(E2)=k−⋅cOx⋅exp(−RTΔG−=(E1)+(1−β)nFΔE)=−nFcOxk−exp(−RTΔG−=(E1)+(1−β)nFΔE)
同理,我们根据反应势能曲线可以推出在E1电势下,氧化反应的活化能 ΔG+=(E1) 就是 Red 与活化络合物的化学势之差,而当电势降低到E2时,氧化反应更不易发生,活化能会升高,具体升高了−βnFΔE (0<β<1),则有
v+(E1)=k+⋅cRed⋅exp(−RTΔG+=(E1))j+(E1)=nFcRedk+exp(−RTΔG+=(E1))v+(E2)=k+⋅cRed⋅exp(−RTΔG+=(E1)−βnFΔE)j+(E2)=nFcRedk+exp(−RTΔG+=(E1)−βnFΔE)
如果令E1=0,并令参比电极的零电势为体系的零电势(这样 ΔG−=(E1)=ΔG+=(E1)=const.),则有
j−(E)j+(E)=−nFcOxk−exp(−RT(1−β)nFE)=nFcRedk+exp(RTβnFE)
当它们相等时,可得到氧化还原对平衡电势 Er:
j−(Er)exp(RTnFEr)RTnFErErEr=−j+(Er)=cRedcOx⋅k+k−=ln(cRedcOx⋅k+k−)=nFRT(lncRedcOx+lnk+k−)=Er0+nFRTlncRedcOx
这就得到了经典的Nernst方程(能斯特方程),当电势为平衡电势时电极的电流密度称为交换电流密度 j0。
接下来,令实际电势 E=Er+η ( η可以是负值)并代入至电流密度表达式,即可得到:
j−(E)j+(E)=−nFcOxk−exp(−RT(1−β)nFEr−RT(1−β)nFη)=nFcRedk+exp(RTβnFEr+RTβnFη)
根据 j0=j−(Er)=−j+(Er),将含 Er的项替换为含 j0的项,可得:
j−(E)j+(E)=−j0exp(−RT(1−β)nFη)=j0exp(RTβnFη)
净电流为还原和氧化电流的代数和:
j=j+(E)+j−(E)=j0[exp(RTβnFη)−exp(RT−(1−β)nFη)]
这就是描述电极上的电流如何随电极电势变化的Butler-Volmer方程(B-V方程)。当 j<0时,表观上发生的是还原反应,此时电极为阴极。
3. Tafel方程的推导、不对称因子和交换电流密度的概念
根据Butler-Volmer方程,我们可以画出过电势与电流密度的关系图。从图中可以看出, β值越接近0.5,曲线就越对称,而随着β接近于0,阴极电流比阳极电流增加得更快;反之,如果β接近于1,则阳极电流比阴极电流增加得更快,总之曲线变得更不对称了。因此我们称β值为不对称因子。
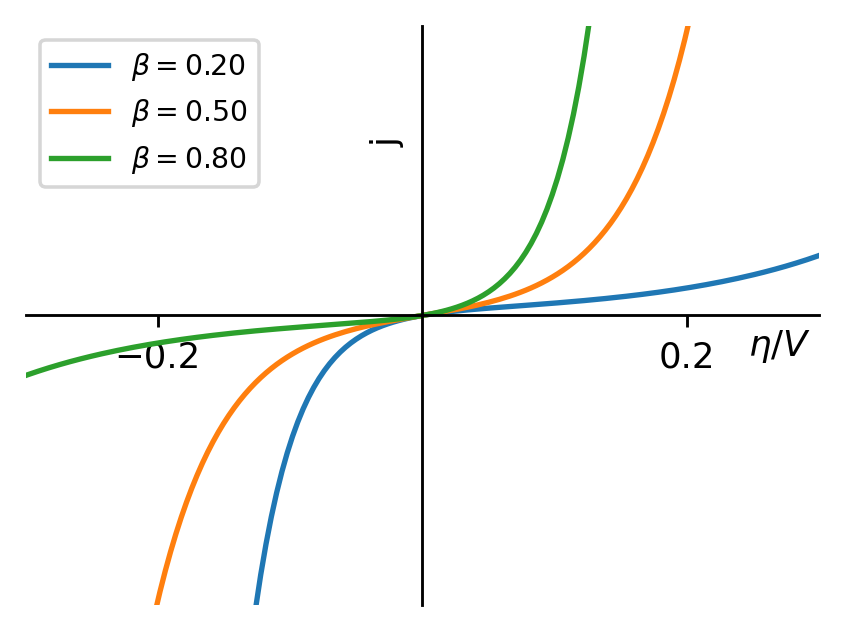 图3:不对称因子改变时,电流密度与过电势的关系
图3:不对称因子改变时,电流密度与过电势的关系
还记得我们推导Butler-Volmer方程时,β值代表什么吗?它恰恰描述了电极电势的变化对中间络合物化学势的影响大小,现在我们将这种影响用图表的方式表达了出来。
当 ∣η∣≫RT/nF时,还原电流相对于氧化电流可以忽略(反之亦然),则Butler-Volmer方程可略为一项。以阴极反应为例, η<0,则
j≈j−(E)=−j0exp(RT−(1−β)nFη)
对上式取绝对值,并将 −(1−β)η写为 (1−β)∣η∣,再以10为底取对数,得到:
lg∣j∣=lgj0+2.3031RT(1−β)nF∣η∣
将上式改写为 ∣η∣=f(j)的形式:
∣η∣=(1−β)nF2.303RTlg∣j∣−(1−β)nF2.303RTlgj0
即:
∣η∣=a+blg∣j∣
对于还原反应,上式可写为
η=−(1−β)nF2.303RTlg(−j)+(1−β)nF2.303RTlgj0
这就得到了Tafel方程。当 β=0.5,n=1时,可得到Tafel方程的斜率 b≈−118mV/dec,也就是说过电势每降低118mV,电流增加1个数量级。
对于阳极发生的氧化反应,我们同样可以得到:
η=βnF2.303RTlgj−βnF2.303RTlgj0
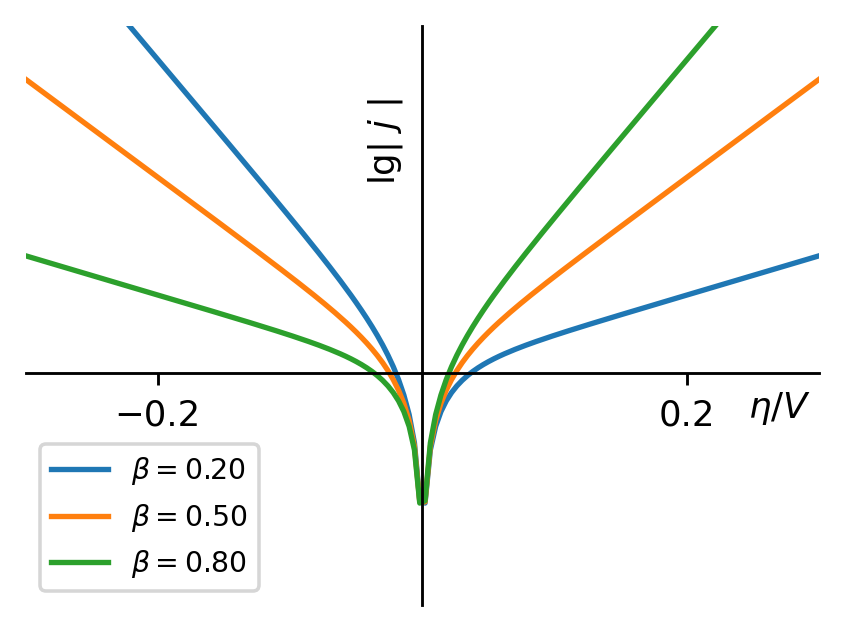 图4:不对称因子改变时,电流密度的对数值与过电势的关系
图4:不对称因子改变时,电流密度的对数值与过电势的关系
在这里,我们必须重申,Tafel方程是在过电势较大的条件下推出的,在过电势很小的情况下,电极可逆程度较大,电流密度与过电势的关系不满足Tafel方程。
当 η<10mV时,可近似运用 ex≈1+x,代入至Butler-Volmer方程中,可得
j=j0RTnFη
也就是说,过电势很小时,电流密度与过电势之间呈线性关系,并且其斜率( =j0nF/RT)与不对称因子无关(很明显,当过电势较小时,中间络合物化学势的变化近似为0)。
交换电流密度值与参与反应的物质浓度以及平衡电势下的活化能有关,它同时影响阳极和阴极电流密度,因此它是电化学过程中重要的基本量之一。所谓的电催化,其核心就是降低反应的活化能,提高 j0。
注意到上式中j具有电流密度的单位,而 η的单位为伏特,则直线斜率的倒数 RT/(j0nF)的单位应是 Ω⋅m2,因此我们称斜率的倒数为电荷转移电阻。j0越大,则电荷转移电阻越小,斜率越大。
j0对Tafel曲线的影响体现在其改变了截距而不是斜率。j0增大会导致阴极过电势的数值升高(绝对值降低)和阳极过电势的降低。
下面我们讨论 j0的测定方法。理论上来讲,可以通过测量极低过电势下的电压-电流关系得到 j0的值,只是由于常见氧化还原反应的j0远低于仪器的检测限,这种方法并不具有普适性。不过,我们可以通过取Tafel曲线的截距 βnF2.303RTlgj0进而求出 j0。
讨论了交换电流密度,我们再来看看影响电化学过程中另外一个重要的物理量——Tafel斜率的影响因素。
从还原反应模型可得到:
b=(1−β)nF2.303RT
可见Tafel斜率与温度、电子转移数和不对称因子有关。
4. 模型的局限性
由于模型是在许多假设下建立的,模型局限性很大,很多时候实际情况不满足模型假设。比如说上述对于Tafel斜率的影响因素的讨论,当反应电子转移数较多,或者分多个步骤进行时(详见本系列下一篇文章:HER 和 OER 反应机理与其 Tafel 斜率推导,如下面的电解水析氧(OER)反应),还要考虑决速步等因素,可能会出现由于决速步的改变导致在不同过电势下具有不同的Tafel斜率的现象,这是我们简单的过渡态理论所不能解释的。

我们再想一想,图4的曲线能否一直向正无穷和负无穷延伸呢?显然是不行的。最直接的原因在于电流密度较大时电极反应将受到传质作用的限制。比如在析氢反应中,电流密度很大时,电极表面产生的氢气气泡会附着在电极表面,阻碍溶液中的氢离子与电极表面的接触;在燃料电池的氧还原反应中,电解质溶液中溶解氧的浓度存在上限,因此还原反应电流将受到溶解氧浓度的限制。不仅如此,经典的双电层模型也存在偏差。因此我们才要不断地对理论进行修正,但电化学的基本原理和过程是不变的。